Modelos de índice de temperatura¶
Objetivos de este cuaderno:
Obtenga una comprensión básica de los modelos de índice de temperatura
Implementar el modelo de índice de temperatura de OGGM para un glaciar de interés
# Plotting libraries and plot style
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set_context('notebook')
sns.set_style('ticks')
import numpy as np
import oggm
from oggm import utils, cfg, workflow, graphics
cfg.initialize()
2022-05-31 14:26:41: oggm.cfg: Reading default parameters from the OGGM `params.cfg` configuration file.
2022-05-31 14:26:41: oggm.cfg: Multiprocessing switched OFF according to the parameter file.
2022-05-31 14:26:41: oggm.cfg: Multiprocessing: using all available processors (N=2)
Algunas configuraciones:
# define a temporary directory to store the required data to
cfg.PATHS['working_dir'] = utils.gettempdir('ti_model')
# set the size of the local glacier map: number of grid points outside the
# glacier boundaries
# increasing this parameter will (significantly!) increase the amount of data
# that needs to be downloaded
cfg.PARAMS['border'] = 10
2022-05-31 14:26:41: oggm.cfg: PARAMS['border'] changed from `40` to `10`.
Fondo¶
El derretimiento de los glaciares influye significativamente en la hidrología de la cuenca. Por lo tanto, es útil contar con predicciones precisas de la escorrentía de las áreas cubiertas por glaciares. En general, hay dos clases de modelos de fusión:
modelos de balance de energía
modelos de índice de temperatura
Los modelos de balance de energía son modelos físicos que cuantifican el fundido como el residuo de la ecuación de balance de energía. Estos modelos requieren mediciones de radiación neta, velocidad del viento, temperatura y propiedades de la superficie para predecir el derretimiento. En un glaciar, las mediciones espacialmente bien resueltas son exigentes y difíciles de mantener. Por lo tanto, un modelo más simple, el modelo de índice de temperatura, es el enfoque más común para modelar el derretimiento de los glaciares.
Los modelos de índice de temperatura asumen una relación empírica entre las temperaturas del aire y las tasas de fusión y son una simplificación de los modelos de balance de energía. El razonamiento es que el derretimiento está influenciado predominantemente por la radiación atmosférica de onda larga y el flujo de calor sensible, componentes del balance de energía que están muy influenciados por la temperatura del aire (Hock, 2003) . La(s) razón(es) principal(es) por las que los modelos de índices de temperatura se usan comúnmente son la amplia disponibilidad de mediciones de la temperatura del aire y la eficiencia computacional.
Configuración del modelo¶
El modelo de índice de temperatura más simple relaciona la cantidad de hielo o nieve derretida \(M\) (mm) con la suma de las temperaturas positivas del aire \(T^+\) (\(^\circ\)C) por un factor de proporcionalidad \(DDF\), el grado -factor de día, para cada \(n\) intervalos de tiempo \(\Delta t\):
Comúnmente, se usa \(\Delta t = 1\) día, de ahí el nombre factor de grado-día. Sin embargo, cualquier otro intervalo de tiempo \(\Delta t\), p. por hora o mensual, se puede utilizar para determinar \(DDF\). En la práctica, el modelo requiere mediciones de la temperatura del aire y el balance de masa del glaciar para estimar \(DDF\); una vez calculado, \(DDF\) se puede usar para predecir el derretimiento midiendo solo la temperatura del aire [(Hock, 2003)](https://www.sciencedirect.com/ ciencia/artículo/pii/S0022169403002579). Sin embargo, este modelo de índice de temperatura, también llamado [(Hock, 2003), no puede predecir el balance de masa de la superficie del glaciar.
Para modelar el balance de masa de la superficie del glaciar, [Marzeion et al., (2012)] (https://www.the-cryosphere.net/6/1295/2012/tc-6-1295-2012.html) desarrolló un modelo de índice de temperatura más sofisticado. El balance de masa mensual \(B_i\) en la elevación \(z\) se calcula como
donde \(P_i^{Solid}\) es la precipitación sólida mensual, \(T_i\) la temperatura promedio mensual, \(T_{Melt}\) la temperatura promedio mensual por encima de la cual se asume el derretimiento del hielo y \(\epsilon\) el residual. Se supone que \(\epsilon\) es un error aleatorio teniendo en cuenta las incertidumbres asociadas con los procesos físicos no resueltos. \(\mu^*\) es la sensibilidad a la temperatura del glaciar y depende de muchos parámetros, en su mayoría específicos del glaciar (por ejemplo, avalanchas, sombreado topográfico, nubosidad, …).
Grados de libertad¶
Entre otros, la sensibilidad a la temperatura \(\mu^*\), el umbral de fusión \(T_{Melt}\) y el umbral implícito de precipitación sólida \(T_{Solid}\) son importantes grados de libertad del modelo - \(T_{Solid} \) es la temperatura media mensual por debajo de la cual se supone que la precipitación es sólida.
Generalmente, \(T_{Melt}\) y \(T_{Solid}\) pueden variar tanto espacial como temporalmente en un glaciar específico. Sin embargo, comúnmente se supone que los dos umbrales \(T_{Melt}\) y \(T_{Solid}\) son constantes. \(T_{Melt}\) y \(T_{Solid}\) influyen significativamente en el balance de masa previsto \(B\) al determinar los meses que se tienen en cuenta en el cálculo.
Tanto \(T_{Melt}\) como \(T_{Solid}\) pueden determinarse mediante un razonamiento físico: sabemos que tanto la nieve se derrite como la precipitación se vuelve sólida alrededor de 0\(^{\circ}\)C. Por lo tanto, los dos umbrales \(T_{Melt}\) y \(T_{Solid}\) están dentro de un rango natural que depende de las condiciones climatológicas en un sitio de glaciar específico.
En OGGM, \(T_{Melt}\) y \(T_{Solid}\) son constantes y puede acceder a los valores predeterminados a través del módulo cfg:
# the default temperature below which solid precipitation is assumed
print('T_solid = {}°C'.format(cfg.PARAMS['temp_all_solid']))
# the default temperature above which melt is assumed to occur
print('T_melt = {}°C'.format(cfg.PARAMS['temp_melt']))
T_solid = 0.0°C
T_melt = -1.0°C
Del mismo modo, puede usar su propio \(T_{Melt}\) y \(T_{Solid}\) si lo desea:
# don't run this ...
# cfg.PARAMS['temp_all_solid'] = 100
# cfg.PARAMS['temp_melt'] = - 273.15
La sensibilidad a la temperatura \(\mu^*\) es específica del glaciar y se determina principalmente mediante técnicas de minimización de errores estadísticos, p. ordinary least squares (OLS). Estas técnicas estadísticas son muy sensibles al tamaño de la muestra: un problema general en glaciología es que el tamaño de la muestra de los registros anuales de balance de masa es bajo para muchos glaciares.
Sin embargo, suponga que un registro de balance de masa de \(100\) por año junto con mediciones de temperatura y precipitación está disponible para un glaciar específico (este es el mejor ejemplo y solo muy pocos glaciares tienen registros tan largos). OLS encontrará un \(\mu^*\) estadísticamente significativo que puede usar felizmente para modelar el balance de masa. Pero, ¿qué sucede si solo usa \( 30 \) años del registro de \( 100 \) años? OLS encontrará otro \(\mu^*\) estadísticamente significativo que es diferente del determinado por el registro anual de \(100\), y se puede encontrar otro \(\mu^*\) estadísticamente significativo para cada subconjunto razonable del registro anual original de \(100\) . Esto implica que \(\mu^*\) es generalmente una sensibilidad a la temperatura \(\mu^*(t)\) dependiente del tiempo.
Por esta razón, OGGM implementa un procedimiento de calibración, introducido por Marzeion et al., (2012), para determinar un glaciar constante específico \(\mu^*\) fuera del tiempo \(\mu^*(t)\) candidatos dependientes. Esta calibración está más allá del alcance de este cuaderno y puede leer sobre ella en detalle [Marzeion et al., (2012) y ver una implementación de ejemplo en OGGM [Marzeion et al., (2012).
Implementación en OGGM¶
Primero, necesitamos definir un directorio de glaciares:
# this may take a while
gdir = workflow.init_glacier_directories([utils.demo_glacier_id('hef')], from_prepro_level=3)[0]
2022-05-31 14:26:42: oggm.workflow: init_glacier_directories from prepro level 3 on 1 glaciers.
2022-05-31 14:26:42: oggm.workflow: Execute entity tasks [gdir_from_prepro] on 1 glaciers
2022-05-31 14:26:42: oggm.utils: Downloading https://cluster.klima.uni-bremen.de/~oggm/gdirs/oggm_v1.4/L3-L5_files/CRU/centerlines/qc3/pcp2.5/no_match/RGI62/b_010/L3/RGI60-11/RGI60-11.00.tar to /github/home/OGGM/download_cache/cluster.klima.uni-bremen.de/~oggm/gdirs/oggm_v1.4/L3-L5_files/CRU/centerlines/qc3/pcp2.5/no_match/RGI62/b_010/L3/RGI60-11/RGI60-11.00.tar...
2022-05-31 14:26:45: oggm.utils: /github/home/OGGM/download_cache/cluster.klima.uni-bremen.de/~oggm/gdirs/oggm_v1.4/L3-L5_files/CRU/centerlines/qc3/pcp2.5/no_match/RGI62/b_010/L3/RGI60-11/RGI60-11.00.tar verified successfully.
Si desea ver el dominio de su modelo, puede trazarlo usando:
# graphics.plot_domain(gdir)
En OGGM, se puede acceder al modelo de índice de temperatura calibrado para cada glaciar a través de la clase PastMassBalance del módulo massbalance:
from oggm.core import massbalance
# this class is the calibrated temperature index model
mb_cal = massbalance.PastMassBalance(gdir)
En este caso,
print('the glacier selected is {},'.format(gdir.name))
the glacier selected is Hintereisferner,
y su sensibilidad a la temperatura calibrada \(\mu^*\) es
print('mu_star = {:2f} mm K^-1 yr^-1.'.format(mb_cal.mu_star))
mu_star = 221.283784 mm K^-1 yr^-1.
De manera similar, el residuo \(\epsilon\) es
print('epsilon = {:2f} mm.'.format(mb_cal.bias))
epsilon = 4.685993 mm.
Datos climáticos¶
De manera predeterminada, el modelo de índice de temperatura se basa en el conjunto de datos climáticos globales CRU TS de \(0.5^{\circ} \times 0.5^{\circ}\). Estos datos climáticos luego se reducen a una cuadrícula de mayor resolución para permitir un conjunto de datos dependiente de la elevación. Se puede acceder a los datos climáticos a la altura de referencia utilizados para impulsar el modelo de índice de temperatura y determinar el \(\mu^*\) calibrado del glaciar seleccionado a través del directorio de glaciares:
fpath = gdir.get_filepath('climate_historical')
print(fpath)
/tmp/OGGM/ti_model/per_glacier/RGI60-11/RGI60-11.00/RGI60-11.00897/climate_historical.nc
Esta es la ruta temporal donde OGGM almacenó sus datos climáticos en su máquina. Puedes leer los datos climáticos usando xarray:
import xarray as xr
climate = xr.open_dataset(fpath)
climate
<xarray.Dataset>
Dimensions: (time: 1416)
Coordinates:
* time (time) datetime64[ns] 1901-10-01 1901-11-01 ... 2019-09-01
Data variables:
prcp (time) float32 109.9 63.26 175.9 109.2 ... 82.08 121.2 187.7 114.2
temp (time) float32 -0.7733 -6.977 -7.38 -7.7 ... 6.3 8.193 7.52 4.213
Attributes:
ref_hgt: 2700.0
ref_pix_lon: 10.75
ref_pix_lat: 46.750000000000014
ref_pix_dis: 5629.5667533869655
climate_source: CRU TS4.04
hydro_yr_0: 1902
hydro_yr_1: 2019
author: OGGM
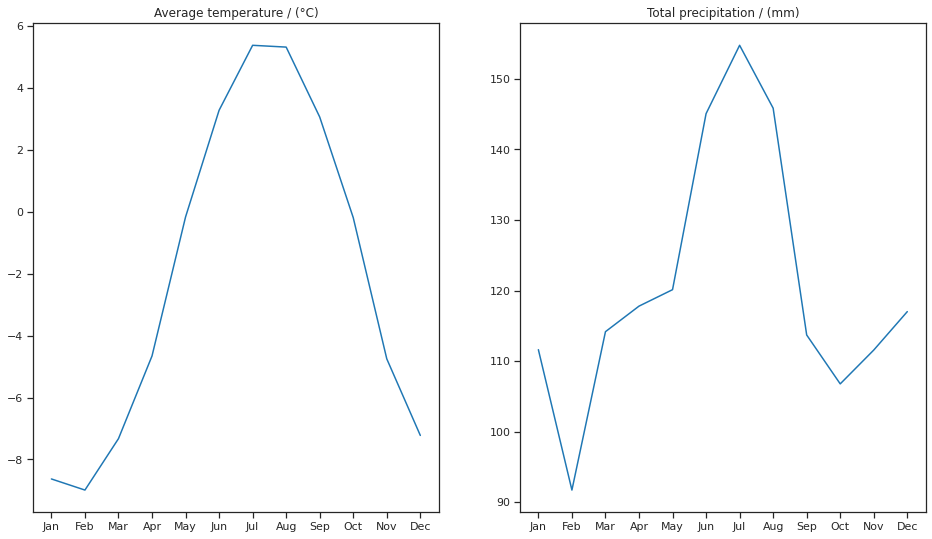
author_info: Open Global Glacier ModelEl conjunto de datos climáticos tiene dos variables, la precipitación total mensual prcp y la temperatura media mensual temp. Calculemos el ciclo medio anual de temperatura media y precipitación total,
annual_cycle = climate.groupby('time.month').mean(dim='time')
y graficarlo, para obtener una vista intuitiva de las condiciones climáticas en el sitio del glaciar seleccionado.
import calendar
fig, ax = plt.subplots(1, 2, figsize=(16, 9))
ax[0].plot(annual_cycle.month, annual_cycle.temp); ax[1].plot(annual_cycle.month, annual_cycle.prcp);
ax[0].set_title('Average temperature / (°C)'); ax[1].set_title('Total precipitation / (mm)');
for a in ax:
a.set_xticks(annual_cycle.month.values)
a.set_xticklabels([calendar.month_abbr[m] for m in annual_cycle.month.values])
Datos de balance de masa de referencia¶
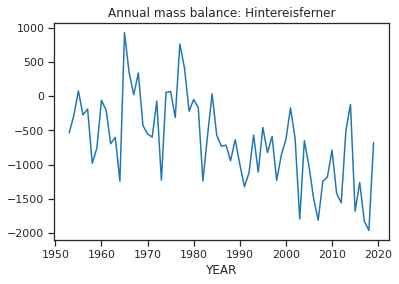
OGGM utiliza datos de balance de masa in situ de la base de datos de fluctuaciones de los glaciares del Servicio Mundial de Monitoreo de Glaciares (WGMS FoGD). La base de datos Fluctuations of Glaciers (FoG) contiene registros anuales de balance de masa de varios cientos de glaciares en todo el mundo. Actualmente, están disponibles 254 series temporales de balance de masa.
Estos datos se envían automáticamente con OGGM y se puede acceder a ellos a través del directorio de glaciares:
# Get the reference mass-balance from the WGMS FoG Database
ref_mb = gdir.get_ref_mb_data()
ref_mb[['ANNUAL_BALANCE']].plot(title='Annual mass balance: {}'.format(gdir.name), legend=False);
¡Prediga el balance de masa!¶
Ahora, estamos listos para calcular el balance de masa del glaciar utilizando el modelo de índice de temperatura: tenemos los parámetros del modelo \(\mu^*\) y \(\epsilon\), los umbrales para el derretimiento y la precipitación sólida \(T_{Melt}\) y \(T_{ Solid}\) y el conjunto de datos climáticos. Lo último que necesitamos definir son las alturas a las que queremos calcular el balance de masa. Aquí, usamos líneas de flujo de glaciares a lo largo de las cuales se calcula el balance de masa:
fls = gdir.read_pickle('inversion_flowlines')
Calcularemos el balance de masa específico en mm w.e. yr\(^{-1}\) para los años en los que se dispone de datos de balance de masa in situ:
print(ref_mb.index.values)
[1953 1954 1955 1956 1957 1958 1959 1960 1961 1962 1963 1964 1965 1966
1967 1968 1969 1970 1971 1972 1973 1974 1975 1976 1977 1978 1979 1980
1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994
1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008
2009 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019]
El balance de masa específico a lo largo de las líneas de flujo dadas se calcula mediante
ref_mb['OGGM (calib)'] = mb_cal.get_specific_mb(fls=fls, year=ref_mb.index.values)
Para este cálculo asumimos una densidad de hielo promedio de
print('rho_ice = {} kg m^-3.'.format(cfg.PARAMS['ice_density']))
rho_ice = 900.0 kg m^-3.
Ahora, podemos comparar el balance de masa real in situ con el balance de masa modelado:
fig, ax = plt.subplots(1, 1)
ax.plot(ref_mb['ANNUAL_BALANCE'], label='Observed')
ax.plot(ref_mb['OGGM (calib)'], label='Modelled')
ax.set_ylabel('Specific mass balance / (mm w.e. y$^{-1}$)')
ax.legend(frameon=False);
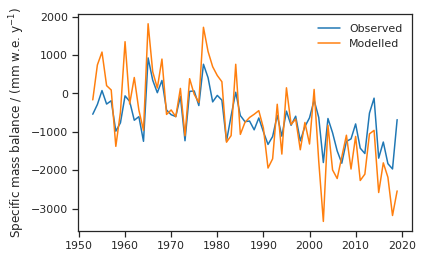
No se ve tan mal, ¿verdad? Para evaluar el rendimiento del modelo, es útil representar los datos en un diagrama de dispersión:
fig, ax = plt.subplots(1, 1)
ax.plot(ref_mb['ANNUAL_BALANCE'], ref_mb['OGGM (calib)'], 'ok');
ax.plot(ref_mb['ANNUAL_BALANCE'], ref_mb['ANNUAL_BALANCE'], '-r');
ax.set_xlim(-3000, 2000)
ax.set_ylim(-3000, 2000)
ax.set_xlabel('Observed');
ax.set_ylabel('OGGM (calib)');
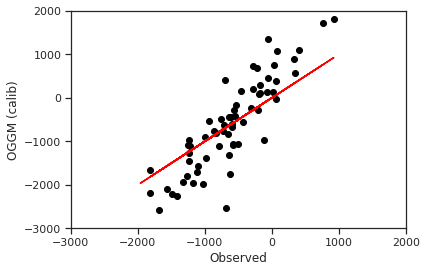
Si los puntos estuvieran alineados a lo largo de la línea roja, el modelo predeciría perfectamente el balance de masa. En general, el modelo sobreestima el balance de masa en magnitud: el diagrama de dispersión muestra una pendiente más pronunciada que la línea roja 1 a 1. Esto se debe a que el balance de masa específico depende no solo del clima sino también de la superficie del glaciar.
OGGM calcula el balance de masa específico como un promedio ponderado del área del glaciar utilizando una geometría de glaciar constante fijada en la fecha Randolph Glacier Inventory, p. \(2003\) para la mayoría de los glaciares de los Alpes europeos. La geometría de los glaciares es en sí misma una función del clima y puede cambiar significativamente con el tiempo. Por lo tanto, suponer una geometría glaciar constante durante un período de tiempo de diferentes condiciones climáticas puede resultar en un sesgo sistemático del modelo:
bias = ref_mb['OGGM (calib)'] - ref_mb['ANNUAL_BALANCE']
fig, ax = plt.subplots(1, 1)
ax.plot(bias);
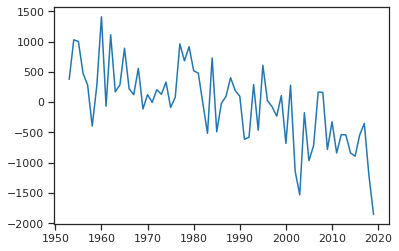
El sesgo es positivo al comienzo de las mediciones in situ y muestra una tendencia negativa. Cuando se mantiene constante el área del glaciar, un sesgo positivo (negativo) significa que la sensibilidad a la temperatura calibrada \(\mu^*\) del glaciar es demasiado baja (alta) durante períodos de tiempo de climas más fríos (más cálidos). Puede encontrar un experimento simple sobre la sensibilidad del balance de masa específico en el cambio climático y el área de la superficie del glaciar en este blog post.
Llévate puntos a casa¶
Hay dos tipos diferentes de modelos de fusión: el modelo de balance de energía y el modelo de índice de temperatura
El modelo de índice de temperatura es la simplificación computacionalmente eficiente del modelo de balance de energía
Los modelos de índice de temperatura asumen una relación empírica entre la temperatura del aire y las tasas de fusión
Los modelos de índice de temperatura se pueden extender para modelar el balance de masa de los glaciares agregando precipitación sólida como parámetro del modelo
El resultado del modelo está significativamente influenciado por la elección de \(T_{Melt}\) y \(T_{Solid}\)
La sensibilidad a la temperatura de un glaciar no es constante en el tiempo \(\mu^* = \mu^*(t)\)
El balance de masa específico es función del clima y de la superficie del glaciar
Referencias¶
Hock R., (2003). Modelado del índice de temperatura de fusión en áreas montañosas. Revista de Hidrología, 281, 104-115. https://doi.org/10.1016/S0022-1694(03)00257-9
Marzeion B., Jarosch A. H. & Hofer M. (2012). Cambio pasado y futuro del nivel del mar a partir del balance de masa superficial de los glaciares. La criosfera, 6, 1295-1322. https://doi.org/10.5194/tc-6-1295-2012
¿Que sigue?¶
xx_markdown_enlace_xx
