Gradientes de balance de masa (MBG) y su influencia en el flujo glaciar¶
En el cuaderno de introducción, mencionamos brevemente el gradiente de balance de masa de un glaciar. Esto es lo que vamos a echar un vistazo más de cerca ahora. Si el concepto de balance de masa es completamente nuevo para usted, lea brevemente sobre él aqui, hasta el párrafo “Entonces, ¿qué es el balance de masa de glaciares?”. En este cuaderno, configuraremos algunos glaciares simples para explorar más a fondo qué características de los glaciares cambian con diferentes gradientes de balance de masa. También veremos los temas de volumen y tiempo de respuesta.
Objetivos de este cuaderno:
El estudiante será capaz de explicar los términos:
Gradiente de balance de masa,
Estado de equilibrio
Tiempo de respuesta.
Primero, tenemos que importar las clases relevantes
from oggm_edu import MassBalance, GlacierBed, Glacier, GlacierCollection
Inicializando el glaciar¶
Comenzamos configurando un glaciar simple con un lecho rocoso lineal (ver edu_intro) para generar un punto de partida para nuestro experimento.
# Bed
bed = GlacierBed(top=3400, bottom=1500, width=400)
# Mass balance
mass_balance = MassBalance(ela=3000, gradient=4)
# Glacier
glacier = Glacier(bed=bed, mass_balance=mass_balance)
Cambiando el gradiente de balance de masa (MBG)¶
El MBG se define como el cambio del balance de masa con altitud ¹. Depende en gran medida del clima en el glaciar ¹.
Echemos un vistazo a los efectos del MBG creando algunos glaciares con diferentes gradientes. En el cuaderno de introducción, nuestro glaciar tenía una pendiente de 4 mm/m, así que agreguemos un glaciar con una pendiente más débil y otro con una pendiente más fuerte.
Volveremos a hacer uso de GlacierCollection para progresar rápidamente y visualizar los glaciares.
collection = GlacierCollection()
# Fill the collection. This time we change the attributes on creation.
collection.fill(glacier, n=3, attributes_to_change=
{'gradient':[0.3, 4, 15]}
)
Creación de un perfil de balance de masa complejo¶
También es posible crear un perfil de balance de masa más complejo. Esto se logra pasando una lista de gradientes y otra lista con la altitud de los puntos de ruptura entre ellos.
# Add complex mb profile
complex_mb = MassBalance(ela=3000, gradient=[3, 7, 10, 15],
breakpoints=[2700, 2250, 1800])
glacier_complex_mb = Glacier(bed=bed, mass_balance=complex_mb)
# Add the new glacier to the collection.
collection.add(glacier_complex_mb)
# Progress collection to the same year.
collection.progress_to_year(300)
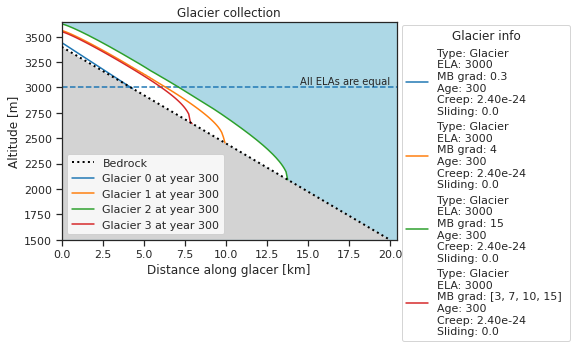
collection.plot()
collection.plot_mass_balance()
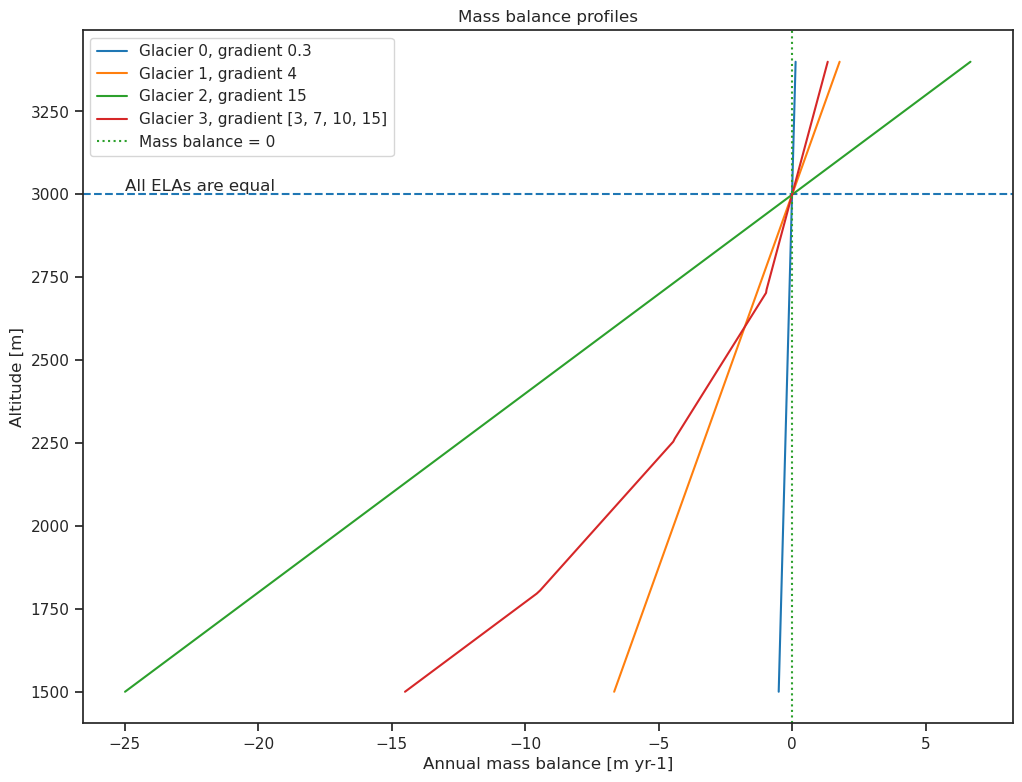
Un gradiente de balance de masa más fuerte (línea más plana en el gráfico anterior) implica un cambio mayor del balance de masa con la altitud. Podemos ver esto en el gráfico anterior: el balance de masa anual apenas cambia con la altitud para el glaciar con el gradiente de balance de masa más débil (azul), mientras que hay una diferencia considerable entre el balance de masa anual superior e inferior para el glaciar con la masa más fuerte. gradiente de equilibrio (verde). Esto a su vez afecta el crecimiento del glaciar. Un fuerte gradiente de balance de masa implica que se agrega más hielo a la zona de acumulación mientras que se extrae más hielo de la zona de ablación cada año en comparación con un glaciar con un gradiente más débil. Esto da como resultado un mayor flujo de hielo y, por lo tanto, el glaciar crece más rápido. Esta es la razón por la cual el glaciar con el gradiente más fuerte exhibe el mayor crecimiento durante nuestros experimentos (Glaciar verde en el gráfico de colección arriba).
Estado de equilibrio¶
Los glaciares cambian su geometría como una forma de adaptarse al clima³. Si la acumulación aumenta, el glaciar crecerá más abajo del ELA para aumentar la ablación. De manera similar, si la temperatura aumenta y la ablación aumenta, la longitud del glaciar disminuirá. Si el clima permanece constante durante un tiempo suficiente, los glaciares alcanzarán un estado de equilibrio con su clima, donde la acumulación = ablación ⁴. Con esto en mente, veremos qué tan rápido nuestros glaciares, con diferentes gradientes, alcanzan este estado y compararemos sus formas:
# We reset the collection.
collection = GlacierCollection()
# Fill the collection. This time we change the attributes on creation.
collection.fill(glacier, n=3, attributes_to_change=
{'gradient':[0.3, 4, 15]}
)
# First we progress the glaciers to equilibrium.
collection.progress_to_equilibrium()
# Plot it
collection.plot()
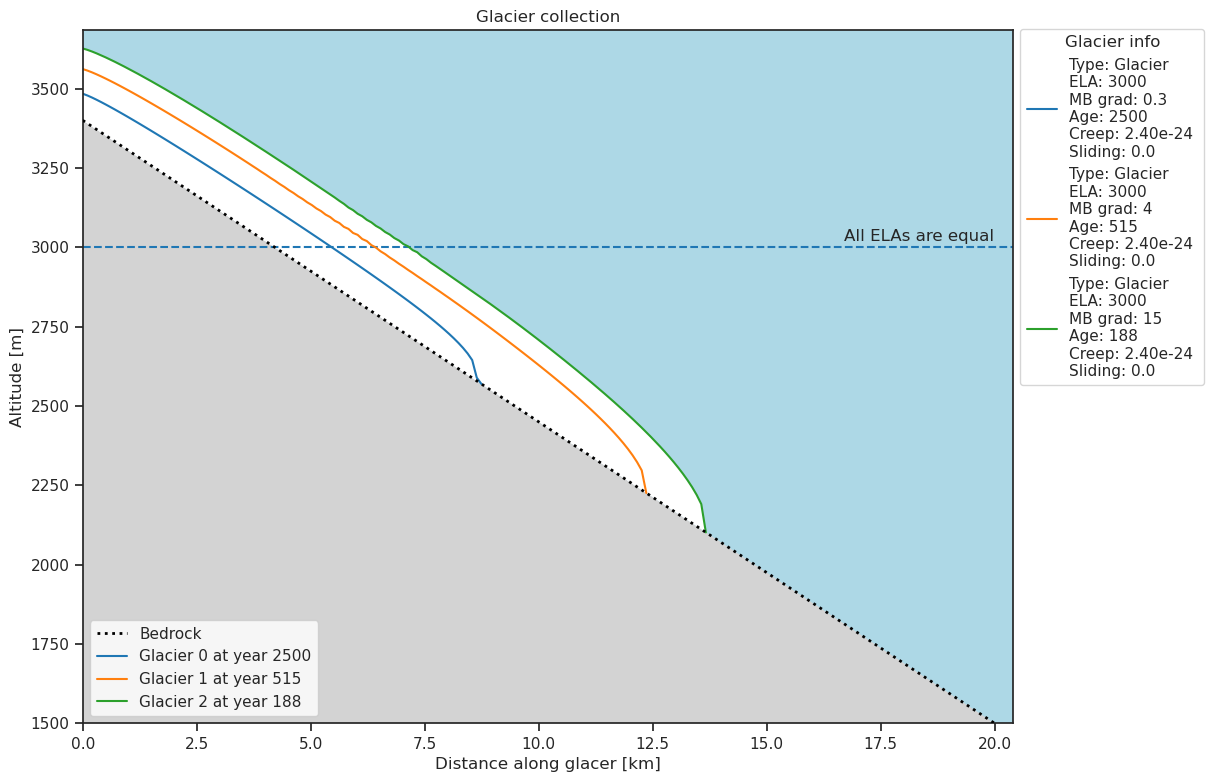
Los diferentes glaciares alcanzan su estado de equilibrio después de un número diferente de años. ¿Qué nos muestra la figura? ¿Qué glaciar es el más grueso y largo? Veamos números específicos:
collection
| Type | Age | Length [m] | Area [km2] | Volume [km3] | Max ice thickness [m] | Response time [yrs] | Bed type | Top [m] | Bottom [m] | Width(s) [m] | Length [km] | ELA [m] | Original ELA [m] | Temperature bias [C] | Gradient [mm/m/yr] | Hemisphere | Ice density [kg/m3] | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Glacier | ||||||||||||||||||
| 0 | Glacier | 2500 | 8700.0 | 3.48 | 0.376760 | 119.836080 | NaN | Linear bed with a constant width | 3400 | 1500 | 400 | 20.0 | 3000 | 3000 | 0 | 0.3 | nh | 900.0 |
| 1 | Glacier | 515 | 12300.0 | 4.92 | 0.931013 | 211.953447 | NaN | Linear bed with a constant width | 3400 | 1500 | 400 | 20.0 | 3000 | 3000 | 0 | 4.0 | nh | 900.0 |
| 2 | Glacier | 188 | 13600.0 | 5.44 | 1.380161 | 283.343538 | NaN | Linear bed with a constant width | 3400 | 1500 | 400 | 20.0 | 3000 | 3000 | 0 | 15.0 | nh | 900.0 |
El glaciar con el gradiente más fuerte alcanza primero el estado de equilibrio. Este es también el glaciar más grande y más largo.
Tiempo de respuesta¶
El tiempo de respuesta del glaciar es el período de tiempo que necesita un glaciar para ajustar su geometría a los cambios en el balance de masa causados por el cambio climático y alcanzar un nuevo estado de equilibrio.
Hay algunas definiciones diferentes para su cálculo, OGGM-Edu usa la definición de Oerlemans (vea la fórmula a continuación) ⁵.
Un glaciar OGGM-Edu tiene un atributo .response_time que se calcula en función de la diferencia entre los dos últimos estados de equilibrio en la historia del glaciar.
Hasta ahora solo te hemos mostrado cómo hacer progresar un glaciar hasta el equilibrio, pero no cómo dejarlo y llegar a un segundo.
Este será el primer paso para obtener el tiempo de respuesta de un glaciar.
Usamos el glaciar desde el comienzo del cuaderno.
# Check the state, everything should be zero/nan here.
glacier
| Attribute | |
|---|---|
| Type | Glacier |
| Age | 0 |
| Length [m] | 0.0 |
| Area [km2] | 0.0 |
| Volume [km3] | 0.0 |
| Max ice thickness [m] | 0.0 |
| Response time [yrs] | NaN |
Primero progresamos el glaciar al equilibrio
glacier.progress_to_equilibrium()
glacier.plot()
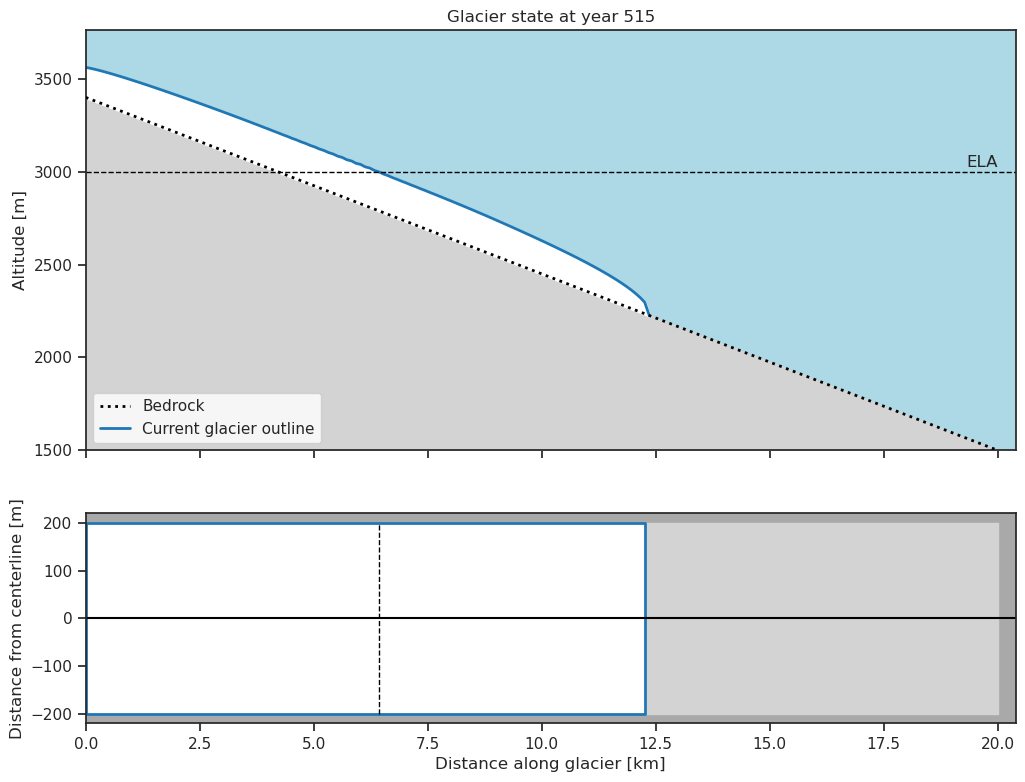
Podemos acceder a los estados de equilibrio almacenados de un glaciar
glacier.eq_states
{515: 3000}
Ahora queremos establecer un escenario de cambio climático para el glaciar.
Esto se hace fácilmente con el método .add_temperature_bias.
Este método toma un sesgo de temperatura deseado (\(+/-\)) y una duración, que especifica cuánto tardará el glaciar en alcanzar el estado climático.
Por ejemplo, si establecemos el sesgo en 1 y la duración en 50, el clima tardará 50 años en calentarse 1 grado.
Cuando un glaciar tiene un escenario de cambio climático, los métodos progress_ funcionarán internamente de manera un poco diferente, pero esto no es algo que notará.
Dado que estamos puramente interesados en la respuesta del glaciar, creamos un escenario de cambio climático con una duración de 1 año.
# Add a climate change scenario
glacier.add_temperature_bias(bias=1., duration=1)
# We can then progress the glacier to equilibrium again
glacier.progress_to_equilibrium()
glacier.plot()
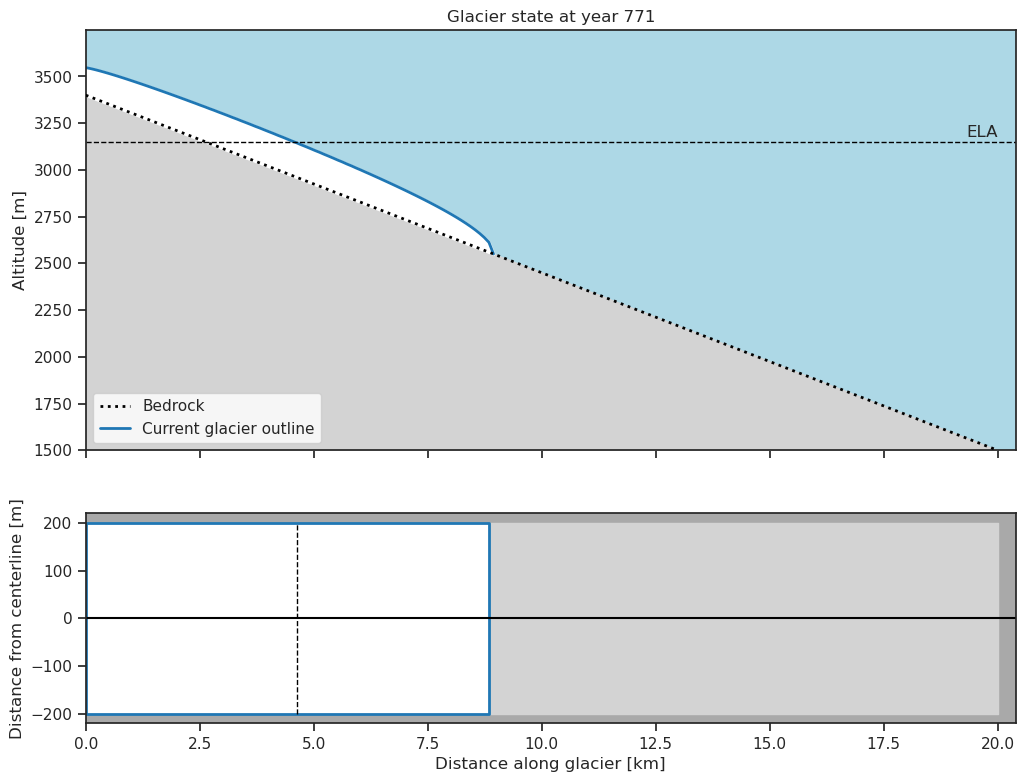
glacier.eq_states
{515: 3000, 771: 3150.0}
El siguiente paso es calcular los tiempos de respuesta de nuestros glaciares. Uno podría pensar que es tan simple como mirar los años anteriores y hacer una simple resta. ¡Sin embargo, éste no es el caso! En realidad, la velocidad a la que cambia un glaciar es cada vez menor y nunca se alcanza realmente un estado de equilibrio completo. Debido a esto, el tiempo de respuesta se considera el tiempo que le ha tomado al glaciar completar la mayor parte del ajuste, más específicamente todo menos un factor de \(1/e\).
Para modelos numéricos como nuestros glaciares, es común usar volume response time, de Oerlemans volume response time:
$\(
\tau = t \left(V=V_2 - \frac{V_2 - V_1}{e}\right)
\)\(
donde \)V_1\( y \)V_2$ corresponden al volumen del glaciar en el estado de equilibrio inicial y nuevo respectivamente.
Afortunadamente, esto lo hace nuestro objeto glaciar, por lo que solo podemos echar un vistazo al atributo .response_time
glacier.response_time
68.0
o simplemente mira la representación
glacier
| Attribute | |
|---|---|
| Type | Glacier |
| Age | 771 |
| Length [m] | 8900.0 |
| Area [km2] | 3.56 |
| Volume [km3] | 0.587687 |
| Max ice thickness [m] | 187.183503 |
| Response time [yrs] | 68.0 |
Ahora que hemos introducido el concepto de tiempo de respuesta, podemos aplicarlo y ver cómo los diferentes gradientes de balance de masa afectan el tiempo de respuesta. Para ello necesitamos una nueva colección.
# Bed
bed = GlacierBed(top=3400, bottom=1500, width=400)
# Mass balance
mass_balance = MassBalance(ela=3000, gradient=4)
# Glacier
glacier = Glacier(bed=bed, mass_balance=mass_balance)
collection = GlacierCollection()
# Fill the collection. This time we change the attributes on creation.
collection.fill(glacier, n=3, attributes_to_change=
{'gradient':[1, 4, 15]}
)
collection.progress_to_equilibrium()
collection
| Type | Age | Length [m] | Area [km2] | Volume [km3] | Max ice thickness [m] | Response time [yrs] | Bed type | Top [m] | Bottom [m] | Width(s) [m] | Length [km] | ELA [m] | Original ELA [m] | Temperature bias [C] | Gradient [mm/m/yr] | Hemisphere | Ice density [kg/m3] | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Glacier | ||||||||||||||||||
| 0 | Glacier | 1397 | 11100.0 | 4.44 | 0.617579 | 156.657761 | NaN | Linear bed with a constant width | 3400 | 1500 | 400 | 20.0 | 3000 | 3000 | 0 | 1 | nh | 900.0 |
| 1 | Glacier | 515 | 12300.0 | 4.92 | 0.931013 | 211.953447 | NaN | Linear bed with a constant width | 3400 | 1500 | 400 | 20.0 | 3000 | 3000 | 0 | 4 | nh | 900.0 |
| 2 | Glacier | 188 | 13600.0 | 5.44 | 1.380161 | 283.343538 | NaN | Linear bed with a constant width | 3400 | 1500 | 400 | 20.0 | 3000 | 3000 | 0 | 15 | nh | 900.0 |
Luego tenemos que configurar un escenario de cambio climático para los glaciares en la colección.
# Same scenario for all the glaciers.
collection.glaciers[0].add_temperature_bias(bias=1., duration=1)
collection.glaciers[1].add_temperature_bias(bias=1., duration=1)
collection.glaciers[2].add_temperature_bias(bias=1., duration=1)
# Progress to equilibrium again
collection.progress_to_equilibrium()
collection
| Type | Age | Length [m] | Area [km2] | Volume [km3] | Max ice thickness [m] | Response time [yrs] | Bed type | Top [m] | Bottom [m] | Width(s) [m] | Length [km] | ELA [m] | Original ELA [m] | Temperature bias [C] | Gradient [mm/m/yr] | Hemisphere | Ice density [kg/m3] | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Glacier | ||||||||||||||||||
| 0 | Glacier | 2035 | 8000.0 | 3.20 | 0.378812 | 134.826943 | 228.0 | Linear bed with a constant width | 3400 | 1500 | 400 | 20.0 | 3150.0 | 3000 | 1.0 | 1 | nh | 900.0 |
| 1 | Glacier | 771 | 8900.0 | 3.56 | 0.587687 | 187.183503 | 68.0 | Linear bed with a constant width | 3400 | 1500 | 400 | 20.0 | 3150.0 | 3000 | 1.0 | 4 | nh | 900.0 |
| 2 | Glacier | 289 | 10000.0 | 4.00 | 0.885816 | 247.787963 | 25.0 | Linear bed with a constant width | 3400 | 1500 | 400 | 20.0 | 3150.0 | 3000 | 1.0 | 15 | nh | 900.0 |
collection.plot_history()
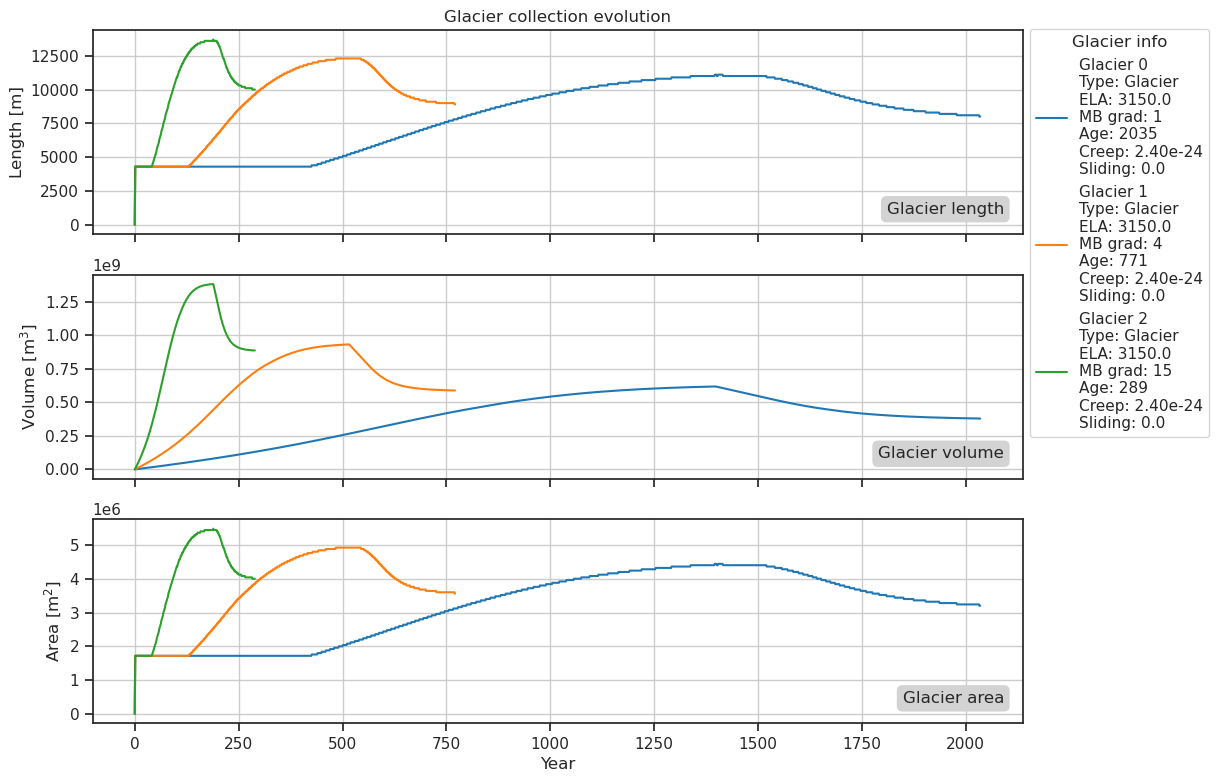
También podemos mirar la historia del estado de uno de los glaciares.
# Plots the glacier outline for the equilibrium states.
collection.glaciers[0].plot_state_history(eq_states=True)
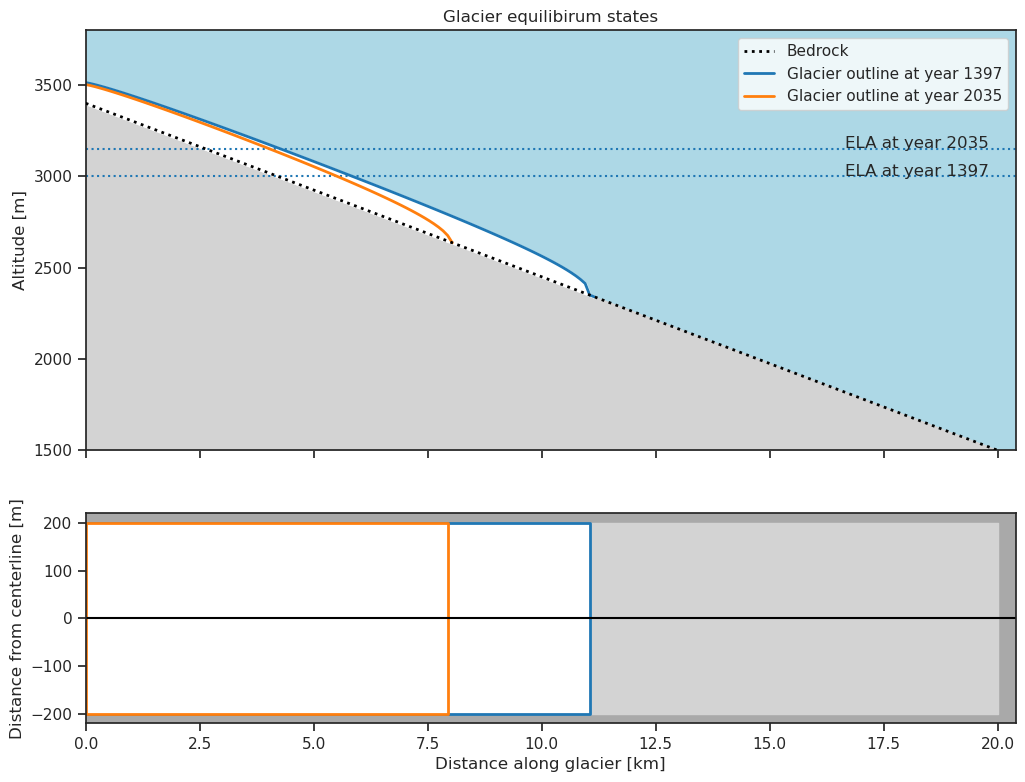
El glaciar con MBG más débil necesita más tiempo para adaptarse a un cambio climático en comparación con los otros glaciares. Por otro lado, el glaciar con el gradiente más fuerte solo necesita alrededor de dos décadas para ajustar su forma al nuevo clima (Un ejemplo del mundo real: el glaciar Franz Josef en Nueva Zelanda⁶)⁶. El tiempo de respuesta de los glaciares con gradientes débiles es en realidad mucho más largo que 200 años, en realidad más cercano a 2000 años.
Referencias¶
¹ Rasmussen, L. A. y Andreassen, L. M. (2005). Gradientes estacionales de balance de masa en Noruega. Revista de Glaciología, 51(175), 601-606. ² Oerlemans, J. y Fortuin, J. P. F. (1992). Sensibilidad de los glaciares y pequeños casquetes polares al efecto invernadero. Ciencia, 258(5079), 115-117. ³Oerlemans, J. (2001). Glaciares y cambio climático. Prensa CRC. ⁴ Enciclopedia de nieve, hielo y glaciares, V.P. Singh, P. Singh y U.K. Haritashya, Editores. 2011, Springer: Dordrecht, Países Bajos. pags. 245-256. ⁵ Oerlemans, J. (1997). Sensibilidad climática del glaciar Franz Josef, Nueva Zelanda, según lo revelado por el modelado numérico. Investigación sobre el Ártico y los Alpes, 29(2), 233-239. ⁶ Anderson, B., Lawson, W. y Owens, I. (2008). Respuesta del glaciar Franz Josef Ka Roimata o Hine Hukatere al cambio climático. Cambio Global y Planetario, 63(1), 23-30. ⁷ Cuffey, K. M. y Paterson, WSB La Física de los Glaciares, 4ª edición, 704 (Academic Press, 2010).
¿Que sigue?¶
xx_markdown_enlace_xx
