.ipynb .pdf

repository open issue suggest edit

Binder JupyterHub

Contents

Los glaciares como recursos hídricos: parte 2 (proyecciones)

Objetivos de este cuaderno:

• ejecutar simulaciones utilizando proyecciones climáticas para explorar el papel de los glaciares como recursos hídricos

Preparando el escenario: la escorrentía de los glaciares y el “pico de agua”

¡Recomendamos enfáticamente ejecutar Parte 1 de este cuaderno antes de continuar!

Configuración

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set_context('notebook')

# One interactive plot below requires Bokeh
# The rest of the notebook works without this dependency
import holoviews as hv
hv.extension('bokeh')
import geoviews as gv
import geoviews.tile_sources as gts

# Temporarily ignore warnings from shapely
import warnings
from shapely.errors import ShapelyDeprecationWarning
warnings.filterwarnings('ignore', category=ShapelyDeprecationWarning)

import xarray as xr
import salem
import numpy as np
import pandas as pd

import oggm.cfg
from oggm import utils, workflow, tasks, graphics

# OGGM options
oggm.cfg.initialize(logging_level='WARNING')
oggm.cfg.PATHS['working_dir'] = utils.gettempdir(dirname='WaterResources')
oggm.cfg.PARAMS['min_ice_thick_for_length'] = 1  # a glacier is when ice thicker than 1m
oggm.cfg.PARAMS['store_model_geometry'] = True

2022-05-31 14:24:36: oggm.cfg: Reading default parameters from the OGGM `params.cfg` configuration file.
2022-05-31 14:24:36: oggm.cfg: Multiprocessing switched OFF according to the parameter file.
2022-05-31 14:24:36: oggm.cfg: Multiprocessing: using all available processors (N=2)
2022-05-31 14:24:37: oggm.cfg: PARAMS['min_ice_thick_for_length'] changed from `0.0` to `1`.
2022-05-31 14:24:37: oggm.cfg: PARAMS['store_model_geometry'] changed from `False` to `True`.

Definir el glaciar con el que jugaremos

Para este cuaderno usamos Hintereisferner, Austria. Algunas otras posibilidades para jugar: -Hintereisferner, Austria: RGI60-11.00897

• Artesonraju, Peru: RGI60-16.02444 -Rikha Samba, Nepal: RGI60-15.04847 -Parlung No. 94, China: RGI60-15.11693 Y prácticamente cualquier glaciar en el que pueda encontrar el RGI Id, p. en el GLIMS viewer! Sin embargo, los grandes glaciares pueden necesitar simulaciones más largas para ver los cambios. Para parámetros de calibración menos inciertos, también recomendamos elegir uno de los muchos glaciares de referencia GLIMS viewer, donde nos aseguramos de que las observaciones del balance de masa coincidan mejor. Comencemos primero con Hintereisferner y al final de este cuaderno se le invitará a probar su glaciar favorito.

# Hintereisferner
rgi_id = 'RGI60-11.00897'

Preparando los datos del glaciar

Esto puede tardar unos minutos en la primera llamada debido a la descarga de los datos necesarios:

# We pick the elevation-bands glaciers because they run a bit faster - but they create more step changes in the area outputs
base_url = 'https://cluster.klima.uni-bremen.de/~oggm/gdirs/oggm_v1.4/L3-L5_files/CRU/elev_bands/qc3/pcp2.5/no_match'
gdir = workflow.init_glacier_directories([rgi_id], from_prepro_level=5, prepro_border=80, prepro_base_url=base_url)[0]

2022-05-31 14:24:37: oggm.workflow: init_glacier_directories from prepro level 5 on 1 glaciers.
2022-05-31 14:24:37: oggm.workflow: Execute entity tasks [gdir_from_prepro] on 1 glaciers

Mapa glaciar interactivo

Un primer vistazo al glaciar de interés. Sugerencia: puede usar el mouse para desplazarse y hacer zoom en el mapa

sh = salem.transform_geopandas(gdir.read_shapefile('outlines'))
(gv.Polygons(sh).opts(fill_color=None, color_index=None) *
 gts.tile_sources['EsriImagery'] * gts.tile_sources['StamenLabels']).opts(width=800, height=500, active_tools=['pan', 'wheel_zoom'])

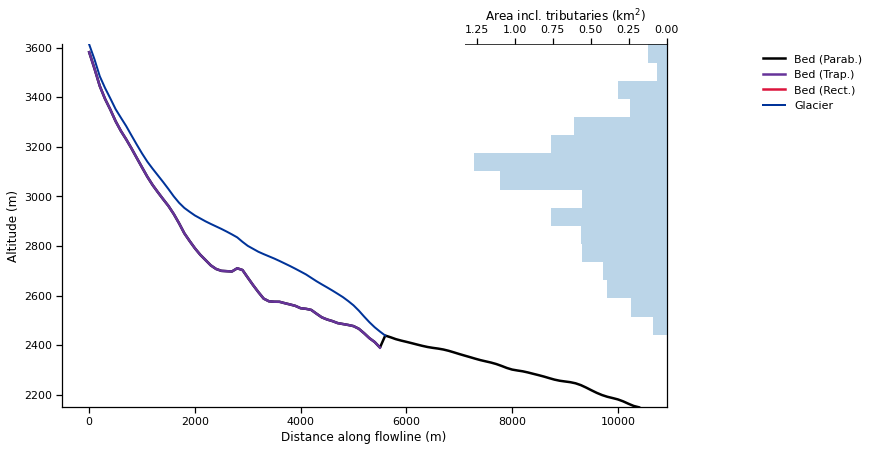
Para OGGM, los glaciares tienen una dimensión de “1,5” a lo largo de su línea de flujo:

fls = gdir.read_pickle('model_flowlines')
graphics.plot_modeloutput_section(fls);

“Ejecución de compromiso”

Ahora estamos listos para ejecutar nuestra primera simulación. Esta es la llamada “ejecución de compromiso”: ¿cuánta pérdida de hielo está “ya comprometida” para este glaciar, incluso si el cambio climático se detuviera hoy? Este es un experimento útil pero puramente teórico: el cambio climático no se detendrá hoy, desafortunadamente. Para obtener más información sobre la pérdida de masa comprometida a escala global, lea Marzeion et al., 2018. Aquí, ejecutamos una simulación durante 100 años con un clima constante basado en los últimos 11 años:

# file identifier where the model output is saved
file_id = '_ct'

# We are using the task run_with_hydro to store hydrological outputs along with the usual glaciological outputs
tasks.run_with_hydro(gdir,
                     run_task=tasks.run_constant_climate,  # which climate? See below for other examples
                     nyears=100,  # length of the simulation
                     y0=2014, halfsize=5,  # For the constant climate, period over which the climate is taken from
                     store_monthly_hydro=True,  # Monthly ouptuts provide additional information
                     output_filesuffix=file_id);  # an identifier for the output file to read it later

Entonces podemos echar un vistazo a la salida:

with xr.open_dataset(gdir.get_filepath('model_diagnostics', filesuffix=file_id)) as ds:
    # The last step of hydrological output is NaN (we can't compute it for this year)
    ds = ds.isel(time=slice(0, -1)).load()

¡Hay muchas variables en este conjunto de datos! Podemos enumerarlos con:

ds

<xarray.Dataset>
Dimensions:                       (time: 100, month_2d: 12)
Coordinates:
  * time                          (time) float64 0.0 1.0 2.0 ... 97.0 98.0 99.0
    hydro_year                    (time) int64 0 1 2 3 4 5 ... 94 95 96 97 98 99
    hydro_month                   (time) int64 1 1 1 1 1 1 1 1 ... 1 1 1 1 1 1 1
    calendar_year                 (time) int64 -1 0 1 2 3 4 ... 94 95 96 97 98
    calendar_month                (time) int64 10 10 10 10 10 ... 10 10 10 10 10
  * month_2d                      (month_2d) int64 1 2 3 4 5 6 7 8 9 10 11 12
    calendar_month_2d             (month_2d) int64 10 11 12 1 2 3 4 5 6 7 8 9
Data variables: (12/21)
    volume_m3                     (time) float64 6.305e+08 ... 8.315e+07
    volume_bsl_m3                 (time) float64 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0
    volume_bwl_m3                 (time) float64 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0
    area_m2                       (time) float64 8.036e+06 ... 2.501e+06
    length_m                      (time) float64 5.6e+03 5.6e+03 ... 1.1e+03
    calving_m3                    (time) float64 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0
    ...                            ...
    liq_prcp_on_glacier           (time) float64 1.034e+10 ... 2.419e+09
    liq_prcp_on_glacier_monthly   (time, month_2d) float64 2.42e+08 ... 2.159...
    snowfall_off_glacier          (time) float64 0.108 5.96e+07 ... 1.191e+10
    snowfall_off_glacier_monthly  (time, month_2d) float64 0.002158 ... 2.46e+08
    snowfall_on_glacier           (time) float64 1.945e+10 ... 6.851e+09
    snowfall_on_glacier_monthly   (time, month_2d) float64 1.969e+09 ... 4.89...
Attributes:
    description:          OGGM model output
    oggm_version:         1.5.4.dev10+g1fca0cb
    calendar:             365-day no leap
    creation_date:        2022-05-31 14:24:38
    water_level:          0
    glen_a:               6.774049426121393e-24
    fs:                   0
    mb_model_class:       MultipleFlowlineMassBalance
    mb_model_hemisphere:  nh

xarray.Dataset

• Dimensions:
  • time: 100
  • month_2d: 12
• Coordinates: (7)
  • time
    (time)
    float64
    0.0 1.0 2.0 3.0 ... 97.0 98.0 99.0

    description :

    Floating hydrological year

    array([ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10., 11., 12., 13.,
           14., 15., 16., 17., 18., 19., 20., 21., 22., 23., 24., 25., 26., 27.,
           28., 29., 30., 31., 32., 33., 34., 35., 36., 37., 38., 39., 40., 41.,
           42., 43., 44., 45., 46., 47., 48., 49., 50., 51., 52., 53., 54., 55.,
           56., 57., 58., 59., 60., 61., 62., 63., 64., 65., 66., 67., 68., 69.,
           70., 71., 72., 73., 74., 75., 76., 77., 78., 79., 80., 81., 82., 83.,
           84., 85., 86., 87., 88., 89., 90., 91., 92., 93., 94., 95., 96., 97.,
           98., 99.])

  • hydro_year
    (time)
    int64
    0 1 2 3 4 5 6 ... 94 95 96 97 98 99

    description :

    Hydrological year

    array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16,
           17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
           34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
           51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
           68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84,
           85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99])

  • hydro_month
    (time)
    int64
    1 1 1 1 1 1 1 1 ... 1 1 1 1 1 1 1 1

    description :

    Hydrological month

    array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
           1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
           1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
           1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
           1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])

  • calendar_year
    (time)
    int64
    -1 0 1 2 3 4 ... 93 94 95 96 97 98

    description :

    Calendar year

    array([-1,  0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15,
           16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32,
           33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49,
           50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66,
           67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83,
           84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98])

  • calendar_month
    (time)
    int64
    10 10 10 10 10 ... 10 10 10 10 10

    description :

    Calendar month

    array([10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10,
           10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10,
           10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10,
           10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10,
           10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10,
           10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10])

  • month_2d
    (month_2d)
    int64
    1 2 3 4 5 6 7 8 9 10 11 12

    array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12])

  • calendar_month_2d
    (month_2d)
    int64
    10 11 12 1 2 3 4 5 6 7 8 9

    array([10, 11, 12,  1,  2,  3,  4,  5,  6,  7,  8,  9])

• Data variables: (21)
  • volume_m3
    (time)
    float64
    6.305e+08 6.129e+08 ... 8.315e+07

    description :

    Total glacier volume

    unit :

    m 3

    array([6.30458361e+08, 6.12919942e+08, 5.95332117e+08, 5.77705456e+08,
           5.60050837e+08, 5.42379011e+08, 5.24700491e+08, 5.07025817e+08,
           4.89364502e+08, 4.71762062e+08, 4.54300037e+08, 4.37008938e+08,
           4.19903976e+08, 4.03004925e+08, 3.86266703e+08, 3.69710079e+08,
           3.53171469e+08, 3.36998052e+08, 3.20850565e+08, 3.04848180e+08,
           2.89093265e+08, 2.73407291e+08, 2.58027632e+08, 2.42765798e+08,
           2.27807825e+08, 2.13144551e+08, 1.98765850e+08, 1.84977369e+08,
           1.72345223e+08, 1.60726303e+08, 1.49703582e+08, 1.40092833e+08,
           1.31469715e+08, 1.24043400e+08, 1.17139065e+08, 1.11292996e+08,
           1.06296648e+08, 1.01612249e+08, 9.79999806e+07, 9.52158829e+07,
           9.27956395e+07, 9.05999029e+07, 8.90737115e+07, 8.84319591e+07,
           8.77851285e+07, 8.71331372e+07, 8.64759364e+07, 8.58134824e+07,
           8.51457342e+07, 8.44726521e+07, 8.43452360e+07, 8.43201556e+07,
           8.42951466e+07, 8.42702070e+07, 8.42453348e+07, 8.42205278e+07,
           8.41957835e+07, 8.41710996e+07, 8.41464734e+07, 8.41219023e+07,
           8.40973836e+07, 8.40729146e+07, 8.40484924e+07, 8.40241142e+07,
           8.39997772e+07, 8.39754783e+07, 8.39512149e+07, 8.39269838e+07,
           8.39027823e+07, 8.38786074e+07, 8.38544563e+07, 8.38303260e+07,
           8.38062137e+07, 8.37821165e+07, 8.37580317e+07, 8.37339563e+07,
           8.37098876e+07, 8.36858227e+07, 8.36617590e+07, 8.36376937e+07,
           8.36136240e+07, 8.35895472e+07, 8.35654595e+07, 8.35413569e+07,
           8.35172367e+07, 8.34930963e+07, 8.34689331e+07, 8.34447445e+07,
           8.34205278e+07, 8.33962805e+07, 8.33720001e+07, 8.33476839e+07,
           8.33233294e+07, 8.32989341e+07, 8.32744955e+07, 8.32500110e+07,
           8.32254782e+07, 8.32008945e+07, 8.31762575e+07, 8.31515646e+07])

  • volume_bsl_m3
    (time)
    float64
    0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0

    description :

    Glacier volume below sea-level

    unit :

    m 3

    array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

  • volume_bwl_m3
    (time)
    float64
    0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0

    description :

    Glacier volume below water-level

    unit :

    m 3

    array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

  • area_m2
    (time)
    float64
    8.036e+06 8.009e+06 ... 2.501e+06

    description :

    Total glacier area

    unit :

    m 2

    array([8036000.        , 8009345.88575447, 7981551.42277013,
           7952306.58566861, 7921531.21777121, 7889220.32720465,
           7855381.78720574, 7820122.10241093, 7783538.74826119,
           7727212.52056573, 7691758.86995448, 7627044.27443308,
           7555506.97389527, 7520450.614186  , 7444725.23707491,
           7409659.49307824, 7373889.92204267, 7293337.94931035,
           7257839.85170964, 7177572.14098374, 7142496.64356524,
           7065173.09901356, 7030649.20266352, 6954404.96561914,
           6878101.18257883, 6845330.04042948, 6772292.91998456,
           6627536.50902401, 6077386.78225554, 5929988.00538531,
           5827280.01492168, 5242089.23662135, 5161932.86900158,
           4892800.17808754, 4835147.06339513, 4295103.99469646,
           4245684.91521036, 4162943.1749889 , 3619276.75115623,
           3546442.27335908, 3488276.67156651, 3484589.63793891,
           2920104.13431304, 2919796.62248985, 2919486.62580877,
           2919174.0746244 , 2918858.9174932 , 2918541.10754404,
           2918220.60127517, 2917897.35774238, 2501391.35517842,
           2501379.20987835, 2501367.10940066, 2501355.05153415,
           2501343.03416145, 2501331.05524368, 2501319.11280847,
           2501307.20494064, 2501295.32977492, 2501283.48549026,
           2501271.67030528, 2501259.88247472, 2501248.12028656,
           2501236.38205962, 2501224.66614167, 2501212.97090773,
           2501201.29475867, 2501189.63611998, 2501177.99344063,
           2501166.36519207, 2501154.74986725, 2501143.14597977,
           2501131.55206305, 2501119.96666947, 2501108.38836964,
           2501096.81575163, 2501085.24742024, 2501073.6819963 ,
           2501062.11811597, 2501050.55443007, 2501038.98960341,
           2501027.42231419, 2501015.85064426, 2501004.2726977 ,
           2500992.68718575, 2500981.09283012, 2500969.48836238,
           2500957.87252347, 2500946.24406314, 2500934.60173942,
           2500922.94431818, 2500911.27057256, 2500899.57928259,
           2500887.86923464, 2500876.13922107, 2500864.3880397 ,
           2500852.61449348, 2500840.81739003, 2500828.99554126,
           2500817.14776298])

  • length_m
    (time)
    float64
    5.6e+03 5.6e+03 ... 1.1e+03 1.1e+03

    description :

    Glacier length

    unit :

    m

    array([5600., 5600., 5600., 5600., 5600., 5600., 5600., 5600., 5600.,
           5400., 5400., 5300., 5200., 5200., 5100., 5100., 5000., 5000.,
           5000., 4900., 4900., 4800., 4800., 4700., 4600., 4600., 4400.,
           4100., 4000., 3800., 3600., 3300., 3100., 2900., 2500., 2400.,
           2300., 2100., 1800., 1700., 1600., 1500., 1200., 1200., 1200.,
           1200., 1200., 1200., 1200., 1100., 1100., 1100., 1100., 1100.,
           1100., 1100., 1100., 1100., 1100., 1100., 1100., 1100., 1100.,
           1100., 1100., 1100., 1100., 1100., 1100., 1100., 1100., 1100.,
           1100., 1100., 1100., 1100., 1100., 1100., 1100., 1100., 1100.,
           1100., 1100., 1100., 1100., 1100., 1100., 1100., 1100., 1100.,
           1100., 1100., 1100., 1100., 1100., 1100., 1100., 1100., 1100.,
           1100.])

  • calving_m3
    (time)
    float64
    0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0

    description :

    Total accumulated calving flux

    unit :

    m 3

    array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

  • calving_rate_myr
    (time)
    float64
    0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0

    description :

    Calving rate

    unit :

    m yr-1

    array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
           0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

  • off_area
    (time)
    float64
    6.127e-05 2.665e+04 ... 5.535e+06

    description :

    Off-glacier area

    unit :

    m 2

    array([6.12738840e-05, 2.66541143e+04, 5.44485773e+04, 8.36934144e+04,
           1.14468782e+05, 1.46779673e+05, 1.80618213e+05, 2.15877898e+05,
           2.52461252e+05, 3.08787479e+05, 3.44241130e+05, 4.08955726e+05,
           4.80493026e+05, 5.15549386e+05, 5.91274763e+05, 6.26340507e+05,
           6.62110078e+05, 7.42662051e+05, 7.78160148e+05, 8.58427859e+05,
           8.93503356e+05, 9.70826901e+05, 1.00535080e+06, 1.08159503e+06,
           1.15789882e+06, 1.19066996e+06, 1.26370708e+06, 1.40846349e+06,
           1.95861322e+06, 2.10601199e+06, 2.20871999e+06, 2.79391076e+06,
           2.87406713e+06, 3.14319982e+06, 3.20085294e+06, 3.74089601e+06,
           3.79031508e+06, 3.87305683e+06, 4.41672325e+06, 4.48955773e+06,
           4.54772333e+06, 4.55141036e+06, 5.11589587e+06, 5.11620338e+06,
           5.11651337e+06, 5.11682593e+06, 5.11714108e+06, 5.11745889e+06,
           5.11777940e+06, 5.11810264e+06, 5.53460864e+06, 5.53462079e+06,
           5.53463289e+06, 5.53464495e+06, 5.53465697e+06, 5.53466894e+06,
           5.53468089e+06, 5.53469280e+06, 5.53470467e+06, 5.53471651e+06,
           5.53472833e+06, 5.53474012e+06, 5.53475188e+06, 5.53476362e+06,
           5.53477533e+06, 5.53478703e+06, 5.53479871e+06, 5.53481036e+06,
           5.53482201e+06, 5.53483363e+06, 5.53484525e+06, 5.53485685e+06,
           5.53486845e+06, 5.53488003e+06, 5.53489161e+06, 5.53490318e+06,
           5.53491475e+06, 5.53492632e+06, 5.53493788e+06, 5.53494945e+06,
           5.53496101e+06, 5.53497258e+06, 5.53498415e+06, 5.53499573e+06,
           5.53500731e+06, 5.53501891e+06, 5.53503051e+06, 5.53504213e+06,
           5.53505376e+06, 5.53506540e+06, 5.53507706e+06, 5.53508873e+06,
           5.53510042e+06, 5.53511213e+06, 5.53512386e+06, 5.53513561e+06,
           5.53514739e+06, 5.53515918e+06, 5.53517100e+06, 5.53518285e+06])

  • on_area
    (time)
    float64
    8.036e+06 8.009e+06 ... 2.501e+06

    description :

    On-glacier area

    unit :

    m 2

    array([8036000.        , 8009345.88575447, 7981551.42277013,
           7952306.58566861, 7921531.21777121, 7889220.32720465,
           7855381.78720574, 7820122.10241093, 7783538.74826119,
           7727212.52056573, 7691758.86995448, 7627044.27443308,
           7555506.97389527, 7520450.614186  , 7444725.23707491,
           7409659.49307824, 7373889.92204267, 7293337.94931035,
           7257839.85170964, 7177572.14098374, 7142496.64356524,
           7065173.09901356, 7030649.20266352, 6954404.96561914,
           6878101.18257883, 6845330.04042948, 6772292.91998456,
           6627536.50902401, 6077386.78225554, 5929988.00538531,
           5827280.01492168, 5242089.23662135, 5161932.86900158,
           4892800.17808754, 4835147.06339513, 4295103.99469646,
           4245684.91521036, 4162943.1749889 , 3619276.75115623,
           3546442.27335908, 3488276.67156651, 3484589.63793891,
           2920104.13431304, 2919796.62248985, 2919486.62580877,
           2919174.0746244 , 2918858.9174932 , 2918541.10754404,
           2918220.60127517, 2917897.35774238, 2501391.35517842,
           2501379.20987835, 2501367.10940066, 2501355.05153415,
           2501343.03416145, 2501331.05524368, 2501319.11280847,
           2501307.20494064, 2501295.32977492, 2501283.48549026,
           2501271.67030528, 2501259.88247472, 2501248.12028656,
           2501236.38205962, 2501224.66614167, 2501212.97090773,
           2501201.29475867, 2501189.63611998, 2501177.99344063,
           2501166.36519207, 2501154.74986725, 2501143.14597977,
           2501131.55206305, 2501119.96666947, 2501108.38836964,
           2501096.81575163, 2501085.24742024, 2501073.6819963 ,
           2501062.11811597, 2501050.55443007, 2501038.98960341,
           2501027.42231419, 2501015.85064426, 2501004.2726977 ,
           2500992.68718575, 2500981.09283012, 2500969.48836238,
           2500957.87252347, 2500946.24406314, 2500934.60173942,
           2500922.94431818, 2500911.27057256, 2500899.57928259,
           2500887.86923464, 2500876.13922107, 2500864.3880397 ,
           2500852.61449348, 2500840.81739003, 2500828.99554126,
           2500817.14776298])

  • melt_off_glacier
    (time)
    float64
    0.108 5.599e+07 ... 1.19e+10

    description :

    Off-glacier melt

    unit :

    kg yr-1

    array([1.08002104e-01, 5.59899766e+07, 1.14508253e+08, 1.75885781e+08,
           2.40107786e+08, 3.07073431e+08, 3.76675722e+08, 4.48660639e+08,
           5.22807996e+08, 6.31201974e+08, 7.03234755e+08, 8.26554474e+08,
           9.62555009e+08, 1.03339012e+09, 1.17727789e+09, 1.24766518e+09,
           1.31901699e+09, 1.47138484e+09, 1.54171839e+09, 1.69316347e+09,
           1.76219113e+09, 1.90786139e+09, 1.97534635e+09, 2.11869671e+09,
           2.26233893e+09, 2.32592583e+09, 2.46349417e+09, 2.73585883e+09,
           3.97932736e+09, 4.27138511e+09, 4.47594434e+09, 5.77206244e+09,
           5.92945094e+09, 6.48857420e+09, 6.59859100e+09, 7.80429840e+09,
           7.89880056e+09, 8.05765591e+09, 9.30102823e+09, 9.45226537e+09,
           9.57044542e+09, 9.57770812e+09, 1.08757026e+10, 1.08764372e+10,
           1.08771760e+10, 1.08779201e+10, 1.08786687e+10, 1.08794220e+10,
           1.08801800e+10, 1.08809427e+10, 1.18961207e+10, 1.18961508e+10,
           1.18961807e+10, 1.18962106e+10, 1.18962403e+10, 1.18962699e+10,
           1.18962994e+10, 1.18963288e+10, 1.18963581e+10, 1.18963873e+10,
           1.18964164e+10, 1.18964455e+10, 1.18964745e+10, 1.18965034e+10,
           1.18965323e+10, 1.18965611e+10, 1.18965899e+10, 1.18966186e+10,
           1.18966472e+10, 1.18966759e+10, 1.18967044e+10, 1.18967330e+10,
           1.18967615e+10, 1.18967900e+10, 1.18968185e+10, 1.18968469e+10,
           1.18968754e+10, 1.18969038e+10, 1.18969322e+10, 1.18969606e+10,
           1.18969890e+10, 1.18970174e+10, 1.18970458e+10, 1.18970743e+10,
           1.18971027e+10, 1.18971312e+10, 1.18971596e+10, 1.18971881e+10,
           1.18972166e+10, 1.18972452e+10, 1.18972738e+10, 1.18973024e+10,
           1.18973310e+10, 1.18973597e+10, 1.18973885e+10, 1.18974173e+10,
           1.18974461e+10, 1.18974750e+10, 1.18975039e+10, 1.18975329e+10])

  • melt_off_glacier_monthly
    (time, month_2d)
    float64
    0.002131 0.00529 ... 2.43e+08

    array([[2.13082718e-03, 5.29026290e-03, 0.00000000e+00, ...,
            0.00000000e+00, 0.00000000e+00, 0.00000000e+00],
           [2.69120222e+06, 2.51638106e+05, 0.00000000e+00, ...,
            1.35152633e+07, 3.99556990e+06, 1.39355323e+06],
           [5.64051421e+06, 5.65960227e+05, 0.00000000e+00, ...,
            2.68676769e+07, 7.19235665e+06, 2.68872950e+06],
           ...,
           [5.49169772e+08, 5.75090350e+07, 0.00000000e+00, ...,
            3.37218884e+09, 1.43312510e+08, 2.43042952e+08],
           [5.49169964e+08, 5.75090350e+07, 0.00000000e+00, ...,
            3.37220353e+09, 1.43315585e+08, 2.43044328e+08],
           [5.49170158e+08, 5.75090349e+07, 0.00000000e+00, ...,
            3.37221826e+09, 1.43318650e+08, 2.43045705e+08]])

  • melt_on_glacier
    (time)
    float64
    3.523e+10 3.519e+10 ... 6.873e+09

    description :

    On-glacier melt

    unit :

    kg yr-1

    array([3.52308373e+10, 3.51938855e+10, 3.51466481e+10, 3.50879129e+10,
           3.50173927e+10, 3.49350926e+10, 3.48408575e+10, 3.47358476e+10,
           3.45877873e+10, 3.43321060e+10, 3.40855147e+10, 3.37742073e+10,
           3.34324711e+10, 3.31965839e+10, 3.28690904e+10, 3.27623735e+10,
           3.23422324e+10, 3.21467500e+10, 3.19259702e+10, 3.15320615e+10,
           3.13813608e+10, 3.09402269e+10, 3.07471847e+10, 3.03107267e+10,
           2.98824764e+10, 2.95436585e+10, 2.88560208e+10, 2.75248296e+10,
           2.53524607e+10, 2.45077000e+10, 2.30169279e+10, 2.08181961e+10,
           1.95711774e+10, 1.85316514e+10, 1.74593476e+10, 1.54804638e+10,
           1.50979414e+10, 1.39674074e+10, 1.19737157e+10, 1.14910706e+10,
           1.11675494e+10, 1.05547491e+10, 8.45873946e+09, 8.46161773e+09,
           8.46455816e+09, 8.46756256e+09, 8.47059351e+09, 8.47364827e+09,
           8.47672551e+09, 7.98388959e+09, 6.87642570e+09, 6.87629586e+09,
           6.87616802e+09, 6.87604230e+09, 6.87591881e+09, 6.87579765e+09,
           6.87567890e+09, 6.87556265e+09, 6.87544895e+09, 6.87533785e+09,
           6.87522939e+09, 6.87512361e+09, 6.87502052e+09, 6.87492015e+09,
           6.87482249e+09, 6.87472756e+09, 6.87463534e+09, 6.87454582e+09,
           6.87445901e+09, 6.87437488e+09, 6.87429341e+09, 6.87421458e+09,
           6.87413838e+09, 6.87406478e+09, 6.87399376e+09, 6.87392529e+09,
           6.87385935e+09, 6.87379592e+09, 6.87373496e+09, 6.87367646e+09,
           6.87362038e+09, 6.87356784e+09, 6.87351879e+09, 6.87347210e+09,
           6.87342775e+09, 6.87338572e+09, 6.87334599e+09, 6.87330853e+09,
           6.87327332e+09, 6.87324036e+09, 6.87320962e+09, 6.87318108e+09,
           6.87315472e+09, 6.87313054e+09, 6.87310851e+09, 6.87308862e+09,
           6.87307086e+09, 6.87305521e+09, 6.87304167e+09, 6.87303021e+09])

  • melt_on_glacier_monthly
    (time, month_2d)
    float64
    9.258e+08 1.396e+07 ... 7.436e+08

    array([[9.25754858e+08, 1.39566847e+07, 0.00000000e+00, ...,
            1.06333179e+10, 1.07607068e+10, 4.96269163e+09],
           [9.28955501e+08, 1.42836401e+07, 0.00000000e+00, ...,
            1.06148017e+10, 1.07417151e+10, 4.96163384e+09],
           [9.32182163e+08, 1.46652997e+07, 0.00000000e+00, ...,
            1.05931803e+10, 1.07195821e+10, 4.95879697e+09],
           ...,
           [2.36614006e+06, 1.18893565e-07, 0.00000000e+00, ...,
            2.42313917e+09, 2.46263915e+09, 7.43547041e+08],
           [2.37223091e+06, 1.18891376e-07, 0.00000000e+00, ...,
            2.42311585e+09, 2.46261492e+09, 7.43560799e+08],
           [2.37834476e+06, 1.19122792e-07, 0.00000000e+00, ...,
            2.42309323e+09, 2.46259138e+09, 7.43574820e+08]])

  • liq_prcp_off_glacier
    (time)
    float64
    0.1191 3.92e+07 ... 8.609e+09

    description :

    Off-glacier liquid precipitation

    unit :

    kg yr-1

    array([1.19118814e-01, 3.91987772e+07, 8.15072067e+07, 1.27143445e+08,
           1.76091140e+08, 2.28286240e+08, 2.83698769e+08, 3.42122485e+08,
           4.03375054e+08, 5.03619341e+08, 5.62884938e+08, 6.79324657e+08,
           8.08426398e+08, 8.67487313e+08, 1.00425315e+09, 1.06381706e+09,
           1.12503171e+09, 1.27122781e+09, 1.33246275e+09, 1.47853412e+09,
           1.53951310e+09, 1.68044969e+09, 1.74092932e+09, 1.88018711e+09,
           2.01937438e+09, 2.07725712e+09, 2.21041071e+09, 2.47460666e+09,
           3.27035057e+09, 3.52464812e+09, 3.70079115e+09, 4.57377083e+09,
           4.71349376e+09, 5.15195131e+09, 5.25563434e+09, 6.05167811e+09,
           6.14035515e+09, 6.28819449e+09, 7.06000392e+09, 7.17873874e+09,
           7.27615824e+09, 7.28256206e+09, 8.07691846e+09, 8.07732371e+09,
           8.07773391e+09, 8.07814833e+09, 8.07856786e+09, 8.07899260e+09,
           8.07942261e+09, 8.07985797e+09, 8.60852245e+09, 8.60853741e+09,
           8.60855232e+09, 8.60856719e+09, 8.60858203e+09, 8.60859684e+09,
           8.60861161e+09, 8.60862634e+09, 8.60864105e+09, 8.60865573e+09,
           8.60867038e+09, 8.60868500e+09, 8.60869960e+09, 8.60871418e+09,
           8.60872874e+09, 8.60874327e+09, 8.60875779e+09, 8.60877230e+09,
           8.60878679e+09, 8.60880127e+09, 8.60881574e+09, 8.60883020e+09,
           8.60884466e+09, 8.60885911e+09, 8.60887355e+09, 8.60888800e+09,
           8.60890244e+09, 8.60891688e+09, 8.60893133e+09, 8.60894579e+09,
           8.60896025e+09, 8.60897472e+09, 8.60898919e+09, 8.60900369e+09,
           8.60901819e+09, 8.60903272e+09, 8.60904726e+09, 8.60906182e+09,
           8.60907640e+09, 8.60909101e+09, 8.60910563e+09, 8.60912029e+09,
           8.60913497e+09, 8.60914968e+09, 8.60916442e+09, 8.60917920e+09,
           8.60919400e+09, 8.60920884e+09, 8.60922372e+09, 8.60923864e+09])

  • liq_prcp_off_glacier_monthly
    (time, month_2d)
    float64
    0.0147 0.0004369 ... 1.315e+09

    array([[1.47034178e-02, 4.36904617e-04, 0.00000000e+00, ...,
            2.25879565e-02, 2.43589710e-02, 1.72791152e-02],
           [2.12997660e+06, 9.42132341e+03, 0.00000000e+00, ...,
            9.47985378e+06, 1.02815687e+07, 5.77571853e+06],
           [4.56110297e+06, 2.32757793e+04, 0.00000000e+00, ...,
            1.95064708e+07, 2.11209508e+07, 1.21207862e+07],
           ...,
           [4.45549173e+08, 1.89197957e+06, 0.00000000e+00, ...,
            2.03786323e+09, 2.19892609e+09, 1.31490694e+09],
           [4.45549173e+08, 1.89197957e+06, 0.00000000e+00, ...,
            2.03786754e+09, 2.19893077e+09, 1.31490890e+09],
           [4.45549173e+08, 1.89197957e+06, 0.00000000e+00, ...,
            2.03787186e+09, 2.19893546e+09, 1.31491086e+09]])

  • liq_prcp_on_glacier
    (time)
    float64
    1.034e+10 1.032e+10 ... 2.419e+09

    description :

    On-glacier liquid precipitation

    unit :

    kg yr-1

    array([1.03403893e+10, 1.03230088e+10, 1.03021737e+10, 1.02776717e+10,
           1.02496044e+10, 1.02181629e+10, 1.01835097e+10, 1.01458010e+10,
           1.01052726e+10, 1.00257987e+10, 9.98714122e+09, 9.89105171e+09,
           9.78230461e+09, 9.74350270e+09, 9.62687172e+09, 9.58739859e+09,
           9.54628175e+09, 9.41984825e+09, 9.37845726e+09, 9.25211841e+09,
           9.21076037e+09, 9.08959806e+09, 9.04863055e+09, 8.92900271e+09,
           8.80919287e+09, 8.77042308e+09, 8.65614057e+09, 8.41006747e+09,
           7.63132132e+09, 7.39314548e+09, 7.23244110e+09, 6.37320659e+09,
           6.24599130e+09, 5.81815315e+09, 5.72431882e+09, 4.93670232e+09,
           4.85529026e+09, 4.71421275e+09, 3.94736888e+09, 3.83257310e+09,
           3.73843861e+09, 3.73498159e+09, 2.94264526e+09, 2.94319763e+09,
           2.94375267e+09, 2.94427830e+09, 2.94480712e+09, 2.94533913e+09,
           2.94587434e+09, 2.94641275e+09, 2.41793204e+09, 2.41795259e+09,
           2.41797306e+09, 2.41799346e+09, 2.41801378e+09, 2.41803404e+09,
           2.41805423e+09, 2.41807437e+09, 2.41809445e+09, 2.41811447e+09,
           2.41813445e+09, 2.41815439e+09, 2.41817428e+09, 2.41819413e+09,
           2.41821394e+09, 2.41823372e+09, 2.41825347e+09, 2.41827318e+09,
           2.41829287e+09, 2.41831254e+09, 2.41833218e+09, 2.41835181e+09,
           2.41837142e+09, 2.41839101e+09, 2.41841059e+09, 2.41843016e+09,
           2.41844972e+09, 2.41846928e+09, 2.41848883e+09, 2.41850838e+09,
           2.41852794e+09, 2.41854749e+09, 2.41856706e+09, 2.41858663e+09,
           2.41860621e+09, 2.41862581e+09, 2.41864542e+09, 2.41866505e+09,
           2.41868471e+09, 2.41870438e+09, 2.41872408e+09, 2.41874380e+09,
           2.41876355e+09, 2.41878334e+09, 2.41880315e+09, 2.41882300e+09,
           2.41884288e+09, 2.41886281e+09, 2.41888277e+09, 2.41890278e+09])

  • liq_prcp_on_glacier_monthly
    (time, month_2d)
    float64
    2.42e+08 2.174e+05 ... 2.159e+08

    array([[2.41996684e+08, 2.17426396e+05, 0.00000000e+00, ...,
            2.84614770e+09, 3.07730415e+09, 1.39049189e+09],
           [2.42988107e+08, 2.45785948e+05, 0.00000000e+00, ...,
            2.83829321e+09, 3.06853772e+09, 1.39002305e+09],
           [2.44118644e+08, 2.77166746e+05, 0.00000000e+00, ...,
            2.82959909e+09, 3.05900370e+09, 1.38887612e+09],
           ...,
           [0.00000000e+00, 0.00000000e+00, 0.00000000e+00, ...,
            8.24415055e+08, 8.93490875e+08, 2.15847650e+08],
           [0.00000000e+00, 0.00000000e+00, 0.00000000e+00, ...,
            8.24413954e+08, 8.93489453e+08, 2.15856318e+08],
           [0.00000000e+00, 0.00000000e+00, 0.00000000e+00, ...,
            8.24412851e+08, 8.93488028e+08, 2.15865004e+08]])

  • snowfall_off_glacier
    (time)
    float64
    0.108 5.96e+07 ... 1.191e+10

    description :

    Off-glacier solid precipitation

    unit :

    kg yr-1

    array([1.08002104e-01, 5.95987284e+07, 1.20314680e+08, 1.83078853e+08,
           2.48204713e+08, 3.15774815e+08, 3.85789953e+08, 4.58061590e+08,
           5.32410756e+08, 6.40948151e+08, 7.13096872e+08, 8.36531588e+08,
           9.72593670e+08, 1.04347445e+09, 1.18739618e+09, 1.25780875e+09,
           1.32917943e+09, 1.48156139e+09, 1.55190553e+09, 1.70335856e+09,
           1.77239222e+09, 1.91806704e+09, 1.98555546e+09, 2.12890846e+09,
           2.27255270e+09, 2.33614115e+09, 2.47371069e+09, 2.74607627e+09,
           3.98954553e+09, 4.28160384e+09, 4.48616351e+09, 5.78228195e+09,
           5.93967071e+09, 6.49879419e+09, 6.60881114e+09, 7.81451868e+09,
           7.90902094e+09, 8.06787637e+09, 9.31124875e+09, 9.46248595e+09,
           9.58066605e+09, 9.58792877e+09, 1.08859233e+10, 1.08866579e+10,
           1.08873967e+10, 1.08881408e+10, 1.08888894e+10, 1.08896427e+10,
           1.08904007e+10, 1.08911635e+10, 1.19063415e+10, 1.19063716e+10,
           1.19064015e+10, 1.19064313e+10, 1.19064610e+10, 1.19064906e+10,
           1.19065201e+10, 1.19065495e+10, 1.19065788e+10, 1.19066081e+10,
           1.19066372e+10, 1.19066663e+10, 1.19066953e+10, 1.19067242e+10,
           1.19067531e+10, 1.19067819e+10, 1.19068107e+10, 1.19068394e+10,
           1.19068680e+10, 1.19068966e+10, 1.19069252e+10, 1.19069538e+10,
           1.19069823e+10, 1.19070108e+10, 1.19070393e+10, 1.19070677e+10,
           1.19070962e+10, 1.19071246e+10, 1.19071530e+10, 1.19071814e+10,
           1.19072098e+10, 1.19072382e+10, 1.19072666e+10, 1.19072951e+10,
           1.19073235e+10, 1.19073519e+10, 1.19073804e+10, 1.19074089e+10,
           1.19074374e+10, 1.19074660e+10, 1.19074946e+10, 1.19075232e+10,
           1.19075518e+10, 1.19075805e+10, 1.19076093e+10, 1.19076380e+10,
           1.19076669e+10, 1.19076958e+10, 1.19077247e+10, 1.19077537e+10])

  • snowfall_off_glacier_monthly
    (time, month_2d)
    float64
    0.002158 0.01464 ... 2.46e+08

    array([[2.15809900e-03, 1.46355954e-02, 1.92997951e-02, ...,
            0.00000000e+00, 0.00000000e+00, 0.00000000e+00],
           [5.20477629e+06, 6.54710999e+06, 8.39540294e+06, ...,
            3.45897997e+05, 3.14573664e+05, 1.74068945e+06],
           [1.04222071e+07, 1.33702963e+07, 1.71499882e+07, ...,
            5.65410039e+05, 5.24670902e+05, 3.23360589e+06],
           ...,
           [1.07763124e+09, 1.35967810e+09, 1.74344160e+09, ...,
            2.61350573e+06, 1.53474708e+06, 2.45997096e+08],
           [1.07763449e+09, 1.35968101e+09, 1.74344532e+09, ...,
            2.61355483e+06, 1.53476703e+06, 2.45998474e+08],
           [1.07763775e+09, 1.35968392e+09, 1.74344905e+09, ...,
            2.61360352e+06, 1.53478649e+06, 2.45999854e+08]])

  • snowfall_on_glacier
    (time)
    float64
    1.945e+10 1.936e+10 ... 6.851e+09

    description :

    On-glacier solid precipitation

    unit :

    kg yr-1

    array([1.94462600e+10, 1.93648430e+10, 1.92826538e+10, 1.91987553e+10,
           1.91127491e+10, 1.90244254e+10, 1.89336509e+10, 1.88406642e+10,
           1.87455909e+10, 1.86162831e+10, 1.85235263e+10, 1.83797414e+10,
           1.82233246e+10, 1.81321848e+10, 1.79681283e+10, 1.78776249e+10,
           1.77861564e+10, 1.76140119e+10, 1.75238238e+10, 1.73526382e+10,
           1.72639836e+10, 1.70985345e+10, 1.70115340e+10, 1.68485510e+10,
           1.66855294e+10, 1.66028280e+10, 1.64463873e+10, 1.61558989e+10,
           1.48954319e+10, 1.45872519e+10, 1.43672536e+10, 1.30573899e+10,
           1.28874935e+10, 1.23177507e+10, 1.21978850e+10, 1.09837502e+10,
           1.08819830e+10, 1.07163657e+10, 9.46802775e+09, 9.31285152e+09,
           9.19138642e+09, 9.18117689e+09, 7.88116233e+09, 7.87947012e+09,
           7.87776603e+09, 7.87608188e+09, 7.87438489e+09, 7.87267487e+09,
           7.87095165e+09, 7.86921510e+09, 6.85385332e+09, 6.85378774e+09,
           6.85372242e+09, 6.85365733e+09, 6.85359246e+09, 6.85352780e+09,
           6.85346334e+09, 6.85339907e+09, 6.85333497e+09, 6.85327104e+09,
           6.85320727e+09, 6.85314364e+09, 6.85308015e+09, 6.85301679e+09,
           6.85295355e+09, 6.85289042e+09, 6.85282740e+09, 6.85276447e+09,
           6.85270162e+09, 6.85263885e+09, 6.85257615e+09, 6.85251352e+09,
           6.85245094e+09, 6.85238840e+09, 6.85232590e+09, 6.85226344e+09,
           6.85220100e+09, 6.85213857e+09, 6.85207615e+09, 6.85201374e+09,
           6.85195132e+09, 6.85188889e+09, 6.85182643e+09, 6.85176394e+09,
           6.85170142e+09, 6.85163884e+09, 6.85157622e+09, 6.85151353e+09,
           6.85145077e+09, 6.85138795e+09, 6.85132504e+09, 6.85126204e+09,
           6.85119896e+09, 6.85113577e+09, 6.85107248e+09, 6.85100907e+09,
           6.85094554e+09, 6.85088189e+09, 6.85081811e+09, 6.85075419e+09])

  • snowfall_on_glacier_monthly
    (time, month_2d)
    float64
    1.969e+09 1.977e+09 ... 4.894e+08

    array([[1.96937202e+09, 1.97652376e+09, 2.53114612e+09, ...,
            1.16237029e+08, 1.17347105e+08, 8.75644360e+08],
           [1.96104584e+09, 1.96993887e+09, 2.52275072e+09, ...,
            1.14265772e+08, 1.15517396e+08, 8.68596785e+08],
           [1.95226675e+09, 1.96307045e+09, 2.51399613e+09, ...,
            1.12713759e+08, 1.14001937e+08, 8.61905735e+08],
           ...,
           [6.88188292e+08, 6.15171112e+08, 7.87704521e+08, ...,
            9.74929409e+07, 1.00699551e+08, 4.89384558e+08],
           [6.88185039e+08, 6.15168204e+08, 7.87700797e+08, ...,
            9.74896838e+07, 1.00696273e+08, 4.89372556e+08],
           [6.88181779e+08, 6.15165289e+08, 7.87697066e+08, ...,
            9.74864197e+07, 1.00692988e+08, 4.89360529e+08]])

• Attributes: (9)

  description :

  OGGM model output

  oggm_version :

  1.5.4.dev10+g1fca0cb

  calendar :

  365-day no leap

  creation_date :

  2022-05-31 14:24:38

  water_level :

  0

  glen_a :

  6.774049426121393e-24

  fs :

  0

  mb_model_class :

  MultipleFlowlineMassBalance

  mb_model_hemisphere :

  nh

Consejo: puede hacer clic en una variable y mostrar su atributo con el botón “página” a la derecha. Las variables time y month_2d son coordenadas, y las otras variables se proporcionan como información adicional (por ejemplo, calendar_month, volveremos a esto), o proporcionan los datos reales. Por ejemplo, podemos trazar la evolución anual del volumen y longitud de nuestro glaciar:

fig, axs = plt.subplots(nrows=2, figsize=(10, 7), sharex=True)
ds.volume_m3.plot(ax=axs[0]);
ds.length_m.plot(ax=axs[1]);
axs[0].set_xlabel(''); axs[0].set_title(f'{rgi_id}'); axs[1].set_xlabel('Years');

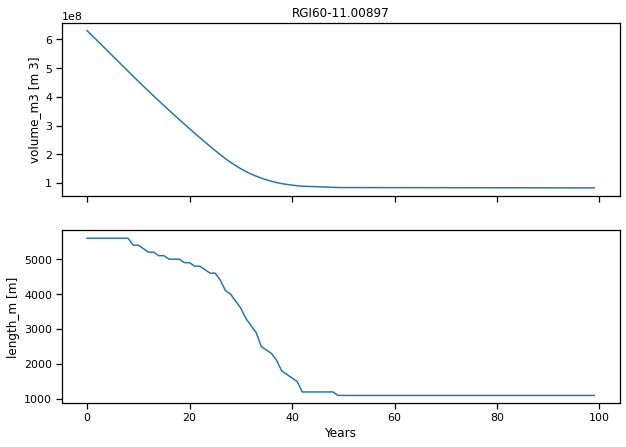
La longitud y el volumen del glaciar disminuyen durante los primeros ~40 años de la simulación: esta es la fase de retroceso del glaciar. Posteriormente, tanto la longitud como el volumen oscilan en torno a un valor más o menos constante indicando que el glaciar ha alcanzado el equilibrio. La diferencia entre el volumen inicial y el volumen de equilibrio se denomina pérdida de masa comprometida. Puede ser bastante alto en los Alpes y depende de muchos factores (como el tamaño del glaciar, la ubicación y el período climático de referencia),

escurrimiento anual

A medida que los glaciares retroceden, contribuyen al aumento del nivel del mar (¡visite la aplicación World Glaciers Explorer OGGM-Edu para obtener más información!). Esto no es lo que nos interesa aquí. De hecho, también tendrán impactos locales importantes: en este cuaderno, veremos su impacto en el flujo de agua. Echemos un vistazo a algunos de los resultados hidrológicos calculados por OGGM. Comenzamos creando un DataFrame de pandas de todas las variables “1D” (anuales):

sel_vars = [v for v in ds.variables if 'month_2d' not in ds[v].dims]
df_annual = ds[sel_vars].to_dataframe()

Luego podemos seleccionar las variables hidrológicas y sumarlas para obtener la escorrentía total anual:

# Select only the runoff variables
runoff_vars = ['melt_off_glacier', 'melt_on_glacier', 'liq_prcp_off_glacier', 'liq_prcp_on_glacier']
# Convert them to megatonnes (instead of kg)
df_runoff = df_annual[runoff_vars] * 1e-9
fig, ax = plt.subplots(figsize=(10, 3.5), sharex=True)
df_runoff.sum(axis=1).plot(ax=ax);
plt.ylabel('Mt'); plt.xlabel('Years'); plt.title(f'Total annual runoff for {rgi_id}');

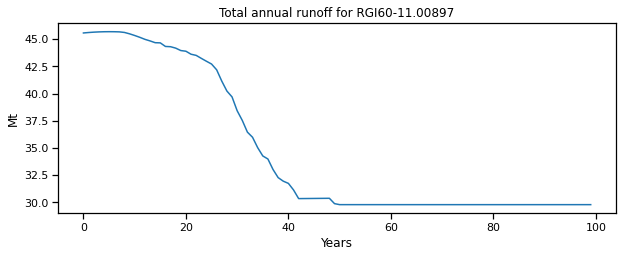
Las variables hidrológicas se calculan sobre la mayor área posible cubierta por hielo glaciar durante la simulación. Esto es equivalente a la escorrentía que se mediría en una estación hidrológica de calibre fijo en el extremo del glaciar. La escorrentía total anual consta de los siguientes componentes:

• fusión fuera del glaciar: la nieve se derrite en áreas que ahora están libres de glaciares (es decir, 0 en el año de mayor extensión del glaciar, en este ejemplo al comienzo de la simulación)

• derretimiento en el glaciar: hielo + nieve estacional derretida en el glaciar

• precipitación líquida dentro y fuera del glaciar (esta última siendo cero en el año de mayor extensión glacial, en este ejemplo al comienzo de la simulación)

f, ax = plt.subplots(figsize=(10, 6));
df_runoff.plot.area(ax=ax, color=sns.color_palette("rocket")); plt.xlabel('Years'); plt.ylabel('Runoff (Mt)'); plt.title(rgi_id);

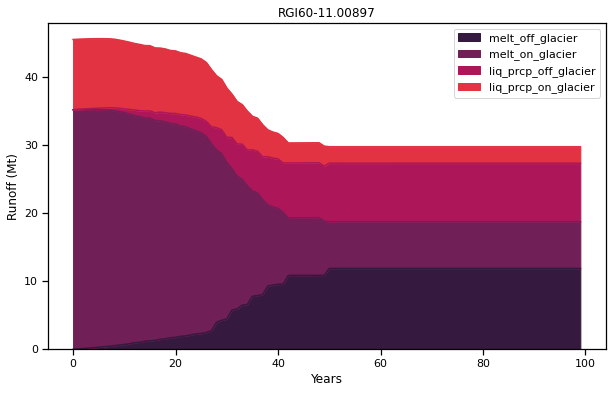
Antes de continuar, recordemos la contribución esperada de los glaciares a la escorrentía. 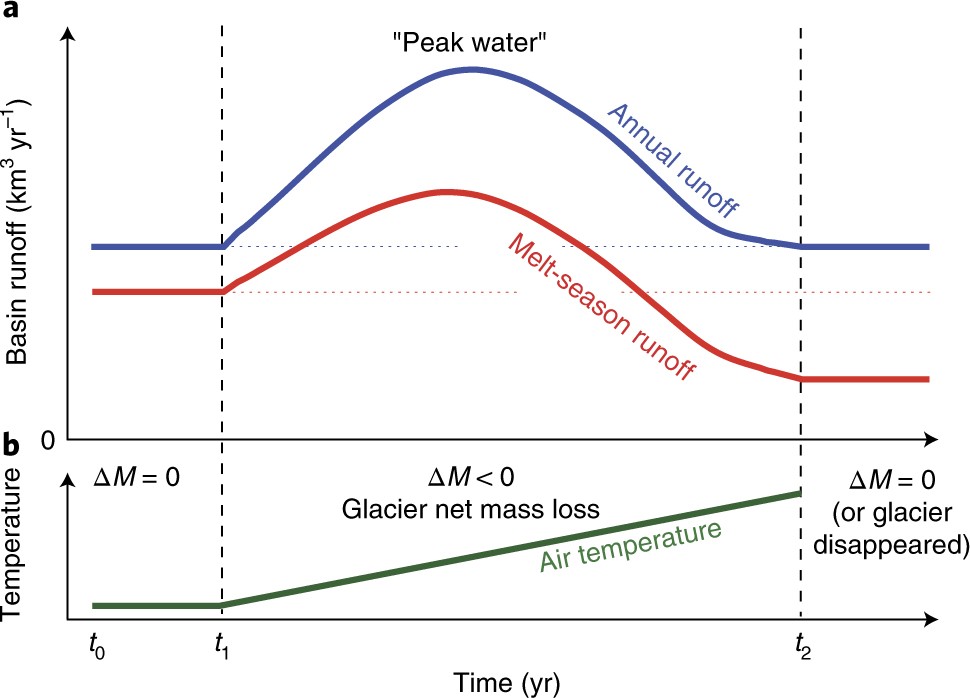Gráfico de Huss & Hock (2018) Preguntas para explorar:

• ¿Dónde aproximadamente en este gráfico se encuentra el glaciar estudiado?

• ¿Puedes explicar la contribución relativa de cada componente, con base en el cuaderno anterior?

La escorrentía total de la cuenca de un glaciar es la suma de las cuatro contribuciones anteriores. Para mostrar que la contribución total del glaciar es de hecho cero (\(\Delta M = 0\)) cuando está en equilibrio, podemos calcularlo a partir del cambio de masa del glaciar:

glacier_mass = ds.volume_m3.to_series() * oggm.cfg.PARAMS['ice_density'] * 1e-9  # In Megatonnes, Mt

glacier_mass.diff().plot()
plt.axhline(y=0, color='k', ls=':')
plt.ylabel('Annual glacier mass change (Mt yr$^{-1}$)')
plt.xlabel('Years'); plt.title('Glacier contribution to annual runoff');

¡Tenga en cuenta que esto no significa que el hielo no se esté derritiendo! En equilibrio, esto significa que el hielo que se derrite cada año sobre el glaciar es reemplazado por nieve en el área de acumulación del glaciar. Esto ilustra bien que los glaciares en equilibrio no son recursos hídricos netos en promedio anual: en el transcurso del año ganan tanta masa como liberan.

escorrentía mensual

Las variables “2D” contienen los mismos datos pero a resolución mensual, con la dimensión (tiempo, mes). Por ejemplo, la escorrentía se puede calcular mismo camino:

# Select only the runoff variables and convert them to megatonnes (instead of kg)
monthly_runoff = (ds['melt_off_glacier_monthly'] + ds['melt_on_glacier_monthly'] +
                  ds['liq_prcp_off_glacier_monthly'] + ds['liq_prcp_on_glacier_monthly'])
monthly_runoff *= 1e-9
monthly_runoff.clip(0).plot(cmap='Blues', cbar_kwargs={'label': 'Mt'}); plt.xlabel('Months'); plt.ylabel('Years');

Pero tenga en cuenta que algo está un poco mal con esto: las coordenadas son meses hidrológicos; mejoremos esto:

# This should work in both hemispheres maybe?
ds_roll = ds.roll(month_2d=ds['calendar_month_2d'].data[0] - 1, roll_coords=True)
ds_roll['month_2d'] = ds_roll['calendar_month_2d']

# Select only the runoff variables and convert them to megatonnes (instead of kg)
monthly_runoff = (ds_roll['melt_off_glacier_monthly'] + ds_roll['melt_on_glacier_monthly'] +
                  ds_roll['liq_prcp_off_glacier_monthly'] + ds_roll['liq_prcp_on_glacier_monthly'])
monthly_runoff *= 1e-9
monthly_runoff.clip(0).plot(cmap='Blues', cbar_kwargs={'label': 'Mt'}); plt.xlabel('Months'); plt.ylabel('Years');

Como podemos ver, la escorrentía es aproximadamente cero durante los meses de invierno, mientras que es relativamente alta durante los meses de verano. Esto implica que el glaciar es una fuente de agua en el verano cuando libera el agua acumulada en el invierno. El ciclo anual cambia a medida que el glaciar retrocede:

monthly_runoff.sel(time=[0, 30, 99]).plot(hue='time');
plt.title('Annual cycle');
plt.xlabel('Month');
plt.ylabel('Runoff (Mt)');

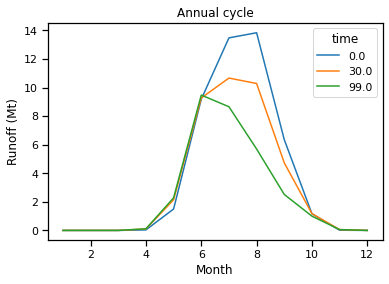
No solo disminuye la escorrentía total durante los meses de verano a medida que avanza la simulación, sino que el mes de máxima escorrentía también se cambia a principios del verano.

Ejecuciones de proyección CMIP5

Ahora ha aprendido a simular y analizar un glaciar específico bajo un clima constante. Ahora daremos un paso más y simularemos dos glaciares diferentes, ubicados en diferentes regiones climáticas, forzados con las proyecciones climáticas de CMIP5. Comenzamos inicializando los directorios de los glaciares:

# We keep Hintereisferner from earlier, but also add a new glacier
rgi_ids = [rgi_id, 'RGI60-15.02420']

gdirs = workflow.init_glacier_directories(rgi_ids, from_prepro_level=5, prepro_border=80, prepro_base_url=base_url)

2022-05-31 14:24:41: oggm.workflow: init_glacier_directories from prepro level 5 on 2 glaciers.
2022-05-31 14:24:41: oggm.workflow: Execute entity tasks [gdir_from_prepro] on 2 glaciers

gdirs ahora contiene dos glaciares, uno en Europa Central y otro en los Himalayas Orientales:

gdirs

[<oggm.GlacierDirectory>
   RGI id: RGI60-11.00897
   Region: 11: Central Europe
   Subregion: 11-01: Alps                            
   Name: Hintereisferner
   Glacier type: Glacier
   Terminus type: Land-terminating
   Status: Glacier or ice cap
   Area: 8.036 km2
   Lon, Lat: (10.7584, 46.8003)
   Grid (nx, ny): (279, 234)
   Grid (dx, dy): (50.0, -50.0),
 <oggm.GlacierDirectory>
   RGI id: RGI60-15.02420
   Region: 15: South Asia East
   Subregion: 15-02: E Himalaya                      
   Glacier type: Glacier
   Terminus type: Land-terminating
   Status: Glacier or ice cap
   Area: 4.401 km2
   Lon, Lat: (90.276115723, 27.926776205)
   Grid (nx, ny): (232, 233)
   Grid (dx, dy): (39.0, -39.0)]

Podemos echar un vistazo rápido al nuevo glaciar:

sh = salem.transform_geopandas(gdirs[1].read_shapefile('outlines'))
(gv.Polygons(sh).opts(fill_color=None, color_index=None) *
 gts.tile_sources['EsriImagery'] * gts.tile_sources['StamenLabels']).opts(width=800, height=500, active_tools=['pan', 'wheel_zoom'])

Reducción climática

Antes de ejecutar nuestra simulación, tenemos que procesar los datos climáticos del glaciar i.i.e. reducir la escala: (Esto puede llevar algún tiempo)

from oggm.shop import gcm_climate
bp = 'https://cluster.klima.uni-bremen.de/~oggm/cmip5-ng/pr/pr_mon_CCSM4_{}_r1i1p1_g025.nc'
bt = 'https://cluster.klima.uni-bremen.de/~oggm/cmip5-ng/tas/tas_mon_CCSM4_{}_r1i1p1_g025.nc'
for rcp in ['rcp26', 'rcp45', 'rcp60', 'rcp85']:
    # Download the files
    ft = utils.file_downloader(bt.format(rcp))
    fp = utils.file_downloader(bp.format(rcp))
    workflow.execute_entity_task(gcm_climate.process_cmip_data, gdirs,
                                 # Name file to recognize it later
                                 filesuffix='_CCSM4_{}'.format(rcp),
                                 # temperature projections
                                 fpath_temp=ft,
                                 # precip projections
                                 fpath_precip=fp,
                                 );

2022-05-31 14:24:55: oggm.workflow: Execute entity tasks [process_cmip_data] on 2 glaciers
2022-05-31 14:25:07: oggm.workflow: Execute entity tasks [process_cmip_data] on 2 glaciers
2022-05-31 14:25:19: oggm.workflow: Execute entity tasks [process_cmip_data] on 2 glaciers
2022-05-31 14:25:31: oggm.workflow: Execute entity tasks [process_cmip_data] on 2 glaciers

Ejecución de proyección

Con la reducción de escala completa, podemos ejecutar las simulaciones forzadas:

for rcp in ['rcp26', 'rcp45', 'rcp60', 'rcp85']:
    rid = '_CCSM4_{}'.format(rcp)
    workflow.execute_entity_task(tasks.run_with_hydro, gdirs,
                                 run_task=tasks.run_from_climate_data, ys=2020,
                                 # use gcm_data, not climate_historical
                                 climate_filename='gcm_data',
                                 # use the chosen scenario
                                 climate_input_filesuffix=rid,
                                 # this is important! Start from 2020 glacier
                                 init_model_filesuffix='_historical',
                                 # recognize the run for later
                                 output_filesuffix=rid,
                                 # add monthly diagnostics
                                 store_monthly_hydro=True);

2022-05-31 14:25:33: oggm.workflow: Execute entity tasks [run_with_hydro] on 2 glaciers
2022-05-31 14:25:34: oggm.workflow: Execute entity tasks [run_with_hydro] on 2 glaciers
2022-05-31 14:25:35: oggm.workflow: Execute entity tasks [run_with_hydro] on 2 glaciers
2022-05-31 14:25:36: oggm.workflow: Execute entity tasks [run_with_hydro] on 2 glaciers

# Create the figure
f, ax = plt.subplots(figsize=(18, 7), sharex=True)
# Loop over all scenarios
for i, rcp in enumerate(['rcp26', 'rcp45', 'rcp60', 'rcp85']):
    file_id = f'_CCSM4_{rcp}'
    # Open the data, gdirs[0] correspond to Hintereisferner.
    with xr.open_dataset(gdirs[0].get_filepath('model_diagnostics', filesuffix=file_id)) as ds:
        # Load the data into a dataframe
        ds = ds.isel(time=slice(0, -1)).load()

    # Select annual variables
    sel_vars = [v for v in ds.variables if 'month_2d' not in ds[v].dims]
    # And create a dataframe
    df_annual = ds[sel_vars].to_dataframe()

    # Select the variables relevant for runoff.
    runoff_vars = ['melt_off_glacier', 'melt_on_glacier', 'liq_prcp_off_glacier', 'liq_prcp_on_glacier']
    # Convert to mega tonnes instead of kg.
    df_runoff = df_annual[runoff_vars].clip(0) * 1e-9
    # Sum the variables each year "axis=1", take the 11 year rolling mean
    # and plot it.
    df_runoff.sum(axis=1).rolling(window=11).mean().plot(ax=ax, label=rcp, color=sns.color_palette("rocket")[i])

ax.set_ylabel('Annual runoff (Mt)'); ax.set_xlabel('Year'); plt.title(gdirs[1].rgi_id); plt.legend();

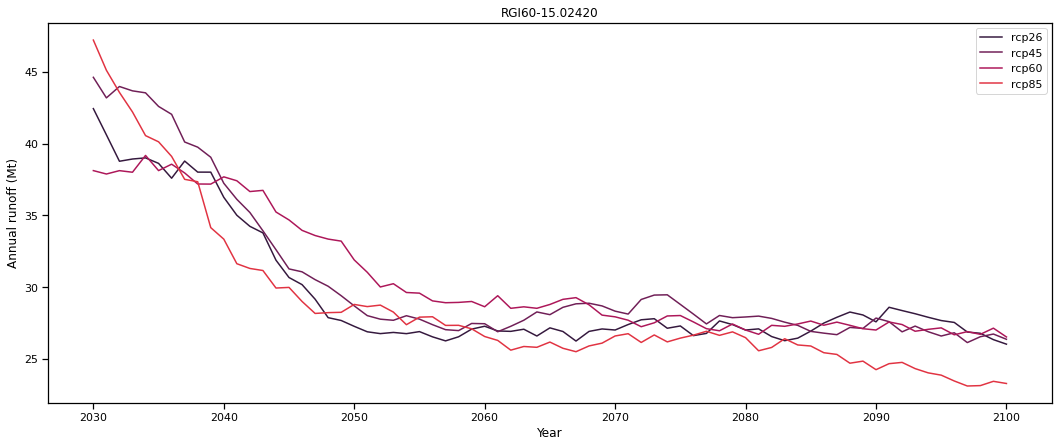
Para Hintereisferner, la escorrentía continúa disminuyendo a lo largo del siglo XXI para todos los escenarios, lo que indica que el pico de agua ya se alcanzó en algún momento del pasado. Este es el caso de muchos glaciares europeos. ¿Qué pasa con nuestro glaciar sin nombre en el Himalaya?

# Create the figure
f, ax = plt.subplots(figsize=(18, 7), sharex=True)
# Loop over all scenarios
for i, rcp in enumerate(['rcp26', 'rcp45', 'rcp60', 'rcp85']):
    file_id = f'_CCSM4_{rcp}'
    # Open the data, gdirs[1] correspond to the unnamed glacier.
    with xr.open_dataset(gdirs[1].get_filepath('model_diagnostics', filesuffix=file_id)) as ds:
        # Load the data into a dataframe
        ds = ds.isel(time=slice(0, -1)).load()

    # Select annual variables
    sel_vars = [v for v in ds.variables if 'month_2d' not in ds[v].dims]
    # And create a dataframe
    df_annual = ds[sel_vars].to_dataframe()

    # Select the variables relevant for runoff.
    runoff_vars = ['melt_off_glacier', 'melt_on_glacier',
                   'liq_prcp_off_glacier', 'liq_prcp_on_glacier']
    # Convert to mega tonnes instead of kg.
    df_runoff = df_annual[runoff_vars].clip(0) * 1e-9
    # Sum the variables each year "axis=1", take the 11 year rolling mean
    # and plot it.
    df_runoff.sum(axis=1).rolling(window=11).mean().plot(ax=ax, label=rcp, color=sns.color_palette("rocket")[i])

ax.set_ylabel('Annual runoff (Mt)'); ax.set_xlabel('Year'); plt.title(rgi_id); plt.legend();

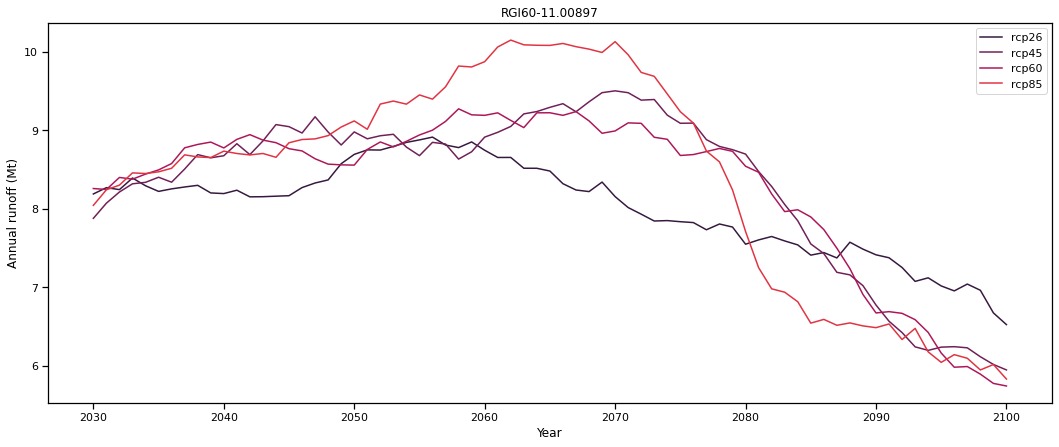
A diferencia de Hintereisferner, estas proyecciones indican que la escorrentía anual aumentará en todos los escenarios para la primera mitad del siglo. Los escenarios de RCP más altos pueden alcanzar el pico de agua más adelante en el siglo, ya que el exceso de derretimiento puede seguir aumentando. Por otro lado, para los escenarios de RCP más bajos, el glaciar podría estar acercándose a un nuevo equilibrio, lo que reduce la escorrentía a principios de siglo (Rounce et. al., 2020). Después de alcanzar el pico de agua (RCP2.6: ~2055, RCP8.5: ~2070 en estas proyecciones), la escorrentía anual comienza a disminuir. Esta disminución se debe a que el glaciar que se encoge ya no puede soportar los altos niveles de derretimiento.

¿Otra ejecución de proyección con sesgo de temperatura o precipitación?

TAREAS: incluya algo sobre cómo el sesgo de temperatura afecta el tamaño del glaciar y la producción de agua de deshielo.

Llévate puntos a casa

• Los glaciares en equilibrio no son recursos hídricos netos: ganan tanta masa como liberan durante un año.

• Sin embargo, tienen una función amortiguadora estacional: liberan agua durante los meses de deshielo.

• El tamaño de un glaciar influye en la disponibilidad de agua aguas abajo durante la estación seca. El impacto es más importante si la temporada de derretimiento (cálida) coincide con la estación seca (ver Kaser et al., 2010).

• Cuando los glaciares se derriten, se convierten en recursos hídricos netos a lo largo del año. El “pico de agua” es el momento en el que el suministro de deshielo de los glaciares alcanza su máximo, es decir, cuando se produce la máxima escorrentía.

Referencias

• Kaser, G., Großhauser, M. y Marzeion, B.: Potencial de contribución de los glaciares a la disponibilidad de agua en diferentes regímenes climáticos, PNAS, 07 (47) 20223-20227, doi:10.1073/pnas.1008162107, 2010

• Huss, M. y Hock, R.: Respuesta hidrológica a escala mundial a la futura pérdida de masa de los glaciares, Nat. Clima Chang., 8(2), 135–140, doi:10.1038/s41558-017-0049-x, 2018.

• Marzeion, B., Kaser, G., Maussion, F. y Champollion, N.: Influencia limitada de la mitigación del cambio climático en la pérdida de masa glaciar a corto plazo, Nat. Clima Chang., 8, doi:10.1038/s41558-018-0093-1, 2018.

• Rounce, D. R., Hock, R., McNabb, R. W., Millan, R., Sommer, C., Braun, M. H., Malz, P., Maussion, F., Mouginot, J., Seehaus, T. C. y Shean, D. E. : Las estimaciones del espesor de los escombros globales distribuidos revelan que los escombros tienen un impacto significativo en el balance de masa de los glaciares, Geophys. Res. Lett., doi:10.1029/2020GL091311, 2021.

¿Que sigue?

xx_markdown_enlace_xx

previous

Los glaciares como recursos hídricos: parte 1 (clima idealizado)