Los glaciares como recursos hídricos: parte 1 (clima idealizado)¶
Nuestros cuadernos anteriores mostraron cómo usar OGGM para responder preguntas teóricas sobre los glaciares, usando experimentos idealizados: el efecto de una pendiente diferente, el concepto de altitud de la línea de equilibrio, el gradiente de balance de masa, etc. Ahora, ¿cómo usamos OGGM para explorar glaciares reales? Este cuaderno nos da una idea.
Objetivos de este cuaderno:
preparar una carrera modelo para un glaciar del mundo real
ejecutar simulaciones utilizando diferentes escenarios climáticos idealizados para explorar el papel de los glaciares como recursos hídricos
comprender el concepto de “pico de agua”
Preparando el escenario: la escorrentía de los glaciares y el “pico de agua”¶
“Si los glaciares se derriten, ya no habrá agua en la montaña”.
Esta es una frase que escuchamos a menudo de personas que conocemos, o a veces incluso en artículos de noticias. De hecho, el papel de los glaciares en el ciclo hidrológico es más complejo que eso. En este cuaderno, exploraremos esta pregunta utilizando escenarios climáticos idealizados aplicados a glaciares reales.
Antes de continuar, echemos un vistazo a la contribución esperada de los glaciares al caudal local. El siguiente gráfico muestra un escenario idealizado donde el clima es primero constante (t\(_0\)-t\(_1\), y el glaciar está en equilibrio con su clima) y luego ocurre un calentamiento (t\(_1\)-t\(_2\)) . Este gráfico presenta algunos puntos muy importantes, que exploraremos juntos en este cuaderno.
Cuando un glaciar está en equilibrio, no contribuye en absoluto a la escorrentía anual.
Cuando el clima se calienta, los glaciares pierden masa. Esta agua contribuye a la escorrentía río abajo, y la escorrentía aumenta.
Si el clima se calienta aún más, los glaciares seguirán perdiendo masa y se volverán significativamente más pequeños. Cuando no quede mucho hielo por derretir cada año (o cuando el clima se estabilice), su contribución será menor hasta volver a ser cero.
En el nuevo equilibrio, la escorrentía anual es la misma que antes, pero la contribución estacional cambió. ¡Ahora volveremos a todos estos puntos juntos, usando OGGM!
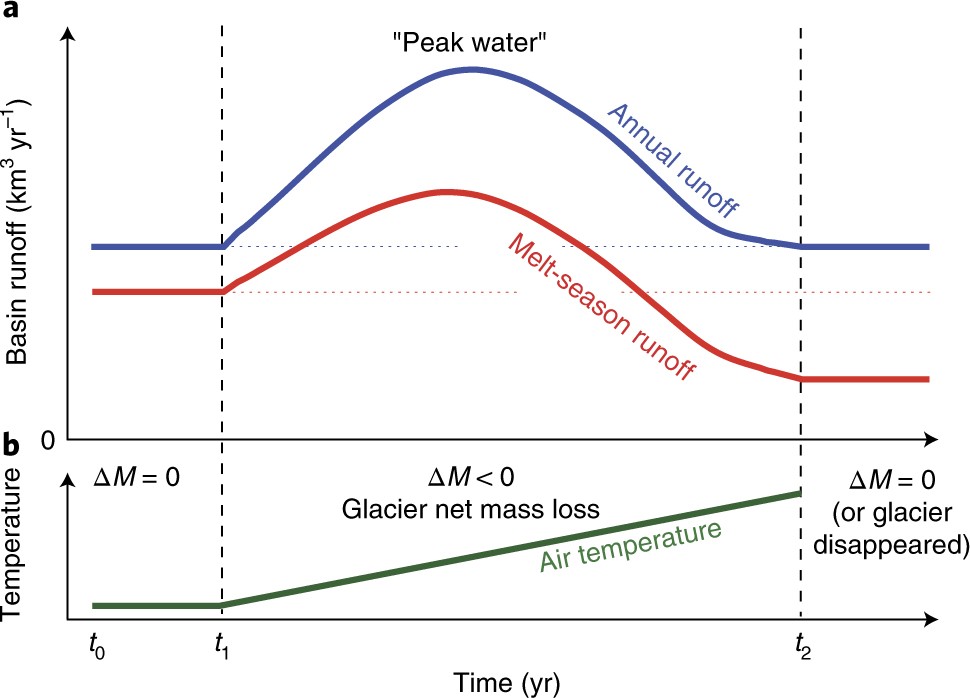 Gráfico de Huss & Hock (2018)
Gráfico de Huss & Hock (2018)
Configuración¶
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set_context('notebook')
# One interactive plot below requires Bokeh
# The rest of the notebook works without this dependency
import holoviews as hv
hv.extension('bokeh')
import geoviews as gv
import geoviews.tile_sources as gts
# Temporarily ignore warnings from shapely
import warnings
from shapely.errors import ShapelyDeprecationWarning
warnings.filterwarnings('ignore', category=ShapelyDeprecationWarning)
import xarray as xr
import salem
import numpy as np
import pandas as pd
import oggm.cfg
from oggm import utils, workflow, tasks, graphics
from oggm_edu.legacy import run_constant_climate_with_bias
# OGGM options
oggm.cfg.initialize(logging_level='WARNING')
oggm.cfg.PATHS['working_dir'] = utils.gettempdir(dirname='WaterResources')
oggm.cfg.PARAMS['min_ice_thick_for_length'] = 1 # a glacier is when ice thicker than 1m
oggm.cfg.PARAMS['store_model_geometry'] = True
2022-05-31 14:23:54: oggm.cfg: Reading default parameters from the OGGM `params.cfg` configuration file.
2022-05-31 14:23:54: oggm.cfg: Multiprocessing switched OFF according to the parameter file.
2022-05-31 14:23:54: oggm.cfg: Multiprocessing: using all available processors (N=2)
2022-05-31 14:24:00: oggm.cfg: PARAMS['min_ice_thick_for_length'] changed from `0.0` to `1`.
2022-05-31 14:24:00: oggm.cfg: PARAMS['store_model_geometry'] changed from `False` to `True`.
Definir el glaciar con el que jugaremos¶
Para este cuaderno usamos Hintereisferner, Austria. Algunas otras posibilidades para jugar: -Hintereisferner, Austria: RGI60-11.00897
Artesonraju, Peru: RGI60-16.02444 -Rikha Samba, Nepal: RGI60-15.04847 -Parlung No. 94, China: RGI60-15.11693 Y prácticamente cualquier glaciar en el que pueda encontrar el RGI Id, p. en el GLIMS viewer! Sin embargo, los grandes glaciares pueden necesitar simulaciones más largas para ver los cambios. Para parámetros de calibración menos inciertos, también recomendamos elegir uno de los muchos glaciares de referencia GLIMS viewer, donde nos aseguramos de que las observaciones del balance de masa coincidan mejor. Comencemos primero con Hintereisferner y al final de este cuaderno se le invitará a probar su glaciar favorito.
# Hintereisferner
rgi_id = 'RGI60-11.00897'
Preparando los datos del glaciar¶
Esto puede tardar unos minutos en la primera llamada debido a la descarga de los datos necesarios:
# We pick the elevation-bands glaciers because they run a bit faster - but they create more step changes in the area outputs
base_url = 'https://cluster.klima.uni-bremen.de/~oggm/gdirs/oggm_v1.4/L3-L5_files/CRU/elev_bands/qc3/pcp2.5/no_match'
gdir = workflow.init_glacier_directories([rgi_id], from_prepro_level=5, prepro_border=80, prepro_base_url=base_url)[0]
2022-05-31 14:24:00: oggm.workflow: init_glacier_directories from prepro level 5 on 1 glaciers.
2022-05-31 14:24:00: oggm.workflow: Execute entity tasks [gdir_from_prepro] on 1 glaciers
Mapa glaciar interactivo¶
Un primer vistazo al glaciar de interés. Sugerencia: puede usar el mouse para desplazarse y hacer zoom en el mapa
sh = salem.transform_geopandas(gdir.read_shapefile('outlines'))
(gv.Polygons(sh).opts(fill_color=None, color_index=None) *
gts.tile_sources['EsriImagery'] * gts.tile_sources['StamenLabels']).opts(width=800, height=500, active_tools=['pan', 'wheel_zoom'])
Para OGGM, los glaciares tienen una dimensión de “1,5” a lo largo de su línea de flujo:
fls = gdir.read_pickle('model_flowlines')
graphics.plot_modeloutput_section(fls);

Generando un glaciar en equilibrio con el clima¶
Preparemos una ejecución con las tareas run_constant_climate_with_bias del paquete oggm_edu. Nos permite ejecutar escenarios idealizados de corrección de temperatura y precipitación de una manera fácil.
Primero, decidamos una evolución de la temperatura:
years = np.arange(400)
temp_bias_ts = pd.Series(years * 0. - 2, index=years)
temp_bias_ts.plot(); plt.xlabel('Year'); plt.ylabel('Temperature bias (°C)');

¡No hay mucho que ver aqui! La variable temp_bias_ts describe un sesgo de temperatura que se aplicará al clima estándar (ver más abajo).
Aquí, el sesgo es de -2 ° todo el tiempo porque queremos ejecutar una carrera llamada “spin-up”, para permitir que el glaciar crezca y asegurarnos de que nuestro glaciar esté en equilibrio dinámico con su clima al final de la simulación. Vamos:
# file identifier where the model output is saved
file_id = '_spinup'
# We are using the task run_with_hydro to store hydrological outputs along with the usual glaciological outputs
tasks.run_with_hydro(gdir, # Run on the selected glacier
temp_bias_ts=temp_bias_ts, # the temperature bias to apply to the average climate
run_task=run_constant_climate_with_bias, # which climate scenario? See following notebook for other examples
y0=2009, halfsize=10, # Period which we will average and constantly repeat
store_monthly_hydro=True, # Monthly ouptuts provide additional information
output_filesuffix=file_id); # an identifier for the output file, to read it later
Bien, hay bastante material nuevo en la celda de arriba. Centrémonos en los puntos más importantes:
ejecutamos el modelo durante 400 años (según lo definido por nuestra serie temporal de temperatura de control)
el modelo se ejecuta con un clima constante promediado durante 21 años (2 veces
halfsize+ 1) para el período 1999-2019aplicamos una polarización en frío de -2°C. De hecho, Hintereisferner está en fuerte desequilibrio con el clima actual y se necesita tal sesgo para que el glaciar crezca (más sobre esto más adelante)
Ahora echemos un vistazo a la salida ahora:
with xr.open_dataset(gdir.get_filepath('model_diagnostics', filesuffix=file_id)) as ds:
# The last step of hydrological output is NaN (we can't compute it for this year)
ds = ds.isel(time=slice(0, -1)).load()
¡Hay muchas variables en este conjunto de datos! Podemos enumerarlos con:
ds
<xarray.Dataset>
Dimensions: (time: 399, month_2d: 12)
Coordinates:
* time (time) float64 0.0 1.0 2.0 ... 397.0 398.0
hydro_year (time) int64 0 1 2 3 4 ... 394 395 396 397 398
hydro_month (time) int64 1 1 1 1 1 1 1 1 ... 1 1 1 1 1 1 1
calendar_year (time) int64 -1 0 1 2 3 ... 394 395 396 397
calendar_month (time) int64 10 10 10 10 10 ... 10 10 10 10 10
* month_2d (month_2d) int64 1 2 3 4 5 6 7 8 9 10 11 12
calendar_month_2d (month_2d) int64 10 11 12 1 2 3 4 5 6 7 8 9
Data variables: (12/21)
volume_m3 (time) float64 6.305e+08 ... 1.024e+09
volume_bsl_m3 (time) float64 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0
volume_bwl_m3 (time) float64 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0
area_m2 (time) float64 8.036e+06 ... 1.023e+07
length_m (time) float64 5.6e+03 5.6e+03 ... 8.4e+03
calving_m3 (time) float64 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0
... ...
liq_prcp_on_glacier (time) float64 6.432e+09 ... 9.347e+09
liq_prcp_on_glacier_monthly (time, month_2d) float64 3.458e+07 ... 9.53...
snowfall_off_glacier (time) float64 4.568e+09 ... 3.106e+07
snowfall_off_glacier_monthly (time, month_2d) float64 4.23e+08 ... 1.815...
snowfall_on_glacier (time) float64 2.336e+10 ... 2.857e+10
snowfall_on_glacier_monthly (time, month_2d) float64 2.284e+09 ... 2.02...
Attributes:
description: OGGM model output
oggm_version: 1.5.4.dev10+g1fca0cb
calendar: 365-day no leap
creation_date: 2022-05-31 14:24:04
water_level: 0
glen_a: 6.774049426121393e-24
fs: 0
mb_model_class: BiasedConstantMassBalance
mb_model_hemisphere: nh
mb_model_rho: 900.0
mb_model_ys: 0
mb_model_ye: 399Consejo: puede hacer clic en una variable y mostrar su atributo con el botón “página” a la derecha.
Las variables time y month_2d son coordenadas, y las otras variables se proporcionan como información adicional (por ejemplo, calendar_month, volveremos a esto), o proporcionan los datos reales. Por ejemplo, podemos trazar la evolución anual del volumen y longitud de nuestro glaciar:
fig, axs = plt.subplots(nrows=2, figsize=(10, 7), sharex=True)
ds.volume_m3.plot(ax=axs[0]);
ds.length_m.plot(ax=axs[1]);
axs[0].set_xlabel(''); axs[0].set_title(f'{rgi_id}'); axs[1].set_xlabel('Years');
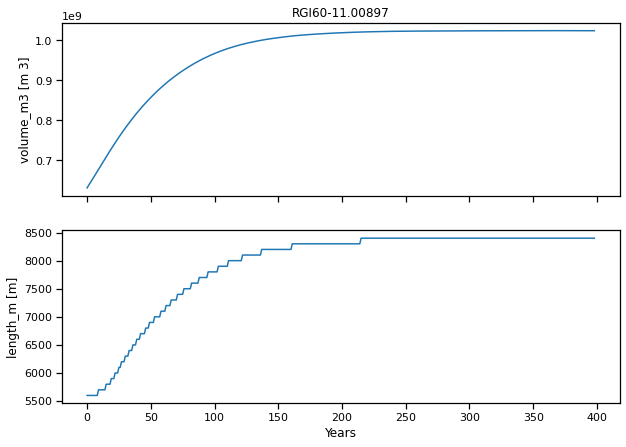
El glaciar crece y casi duplica su volumen. Después de 400 años, está en equilibrio. Esta simulación de rotación no se analizará más: saltemos al corazón del tema: ¿qué sucede con la escorrentía de los glaciares cuando el clima se está calentando?
Simulación de cambio climático¶
Comenzamos generando un escenario de cambio de temperatura. Definimos un período corto de temperatura constante (a -2°C, para ser coherentes con lo anterior), seguido de un aumento lineal (2,5 grados en unos 150 años) y una estabilización:
ny_s = 50 # Start
ny_t = 150 # Trend
ny_e = 102 # Stabilisation
temp_bias_ts = np.concatenate([np.full(ny_s, -2.), np.linspace(-2, 0.5, ny_t), np.full(ny_e, 0.5)])
temp_bias_ts = pd.Series(temp_bias_ts, index=np.arange(ny_s + ny_t + ny_e))
temp_bias_ts.plot(); plt.xlabel('Year'); plt.ylabel('Temperature bias (°C)');
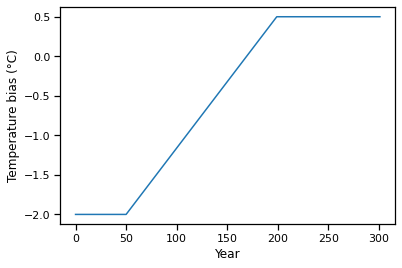
# file identifier where the model output is saved
file_id = '_lin_temp'
# We are using the task run_with_hydro to store hydrological outputs along with the usual glaciological outputs
tasks.run_with_hydro(gdir,
temp_bias_ts=temp_bias_ts, # the temperature bias timeseries we just created
run_task=run_constant_climate_with_bias, # which climate scenario? See following notebook for other examples
y0=2009, halfsize=10, # Period which we will average and constantly repeat
store_monthly_hydro=True, # Monthly ouptuts provide additional information
init_model_filesuffix='_spinup', # We want to start from the glacier in equibrium we created earlier
output_filesuffix=file_id); # an identifier for the output file, to read it later
Echemos un vistazo a la evolución de nuestro glaciar:
with xr.open_dataset(gdir.get_filepath('model_diagnostics', filesuffix=file_id)) as ds:
# The last step of hydrological output is NaN (we can't compute it for this year)
ds = ds.isel(time=slice(0, -1)).load()
fig, axs = plt.subplots(nrows=3, figsize=(10, 7), sharex=True)
ds.volume_m3.plot(ax=axs[0]);
ds.length_m.plot(ax=axs[1]);
temp_bias_ts.plot(ax=axs[2], c='C3');
axs[0].set_xlabel(''); axs[0].set_title(f'{rgi_id}'); axs[1].set_xlabel(''); axs[2].set_xlabel('Years'); axs[2].set_ylabel('Temperature bias (°C)');
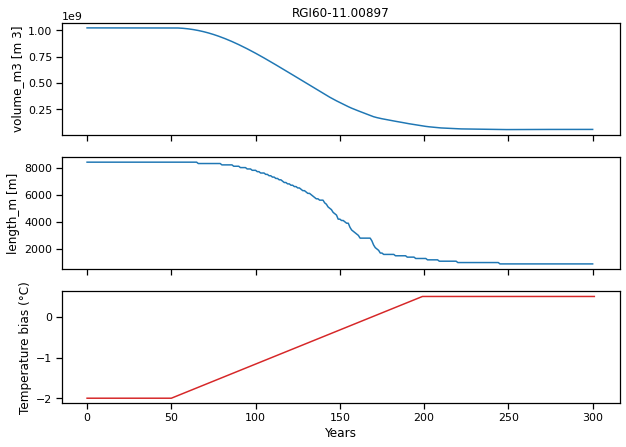
En este escenario, el glaciar se derretiría casi por completo (pierde alrededor del 90% de su volumen). Tenga en cuenta también que el glaciar continúa ajustándose después de que la temperatura se ha estabilizado. ¿Cuáles son las implicaciones para la escorrentía río abajo?
escurrimiento anual¶
A medida que los glaciares retroceden, contribuyen al aumento del nivel del mar (¡visite la aplicación World Glaciers Explorer OGGM-Edu para obtener más información!). Esto no es lo que nos interesa aquí. De hecho, también tendrán impactos locales importantes: en este cuaderno, veremos su impacto en el flujo de agua. Echemos un vistazo a algunos de los resultados hidrológicos calculados por OGGM. Comenzamos creando un marco de datos de pandas de todas las variables “1D” (anuales) en el conjunto de datos de salida:
sel_vars = [v for v in ds.variables if 'month_2d' not in ds[v].dims]
df_annual = ds[sel_vars].to_dataframe()
Luego podemos seleccionar las variables hidrológicas y sumarlas para obtener la escorrentía total anual:
# Select only the runoff variables
runoff_vars = ['melt_off_glacier', 'melt_on_glacier', 'liq_prcp_off_glacier', 'liq_prcp_on_glacier']
# Convert them to megatonnes (instead of kg)
df_runoff = df_annual[runoff_vars] * 1e-9
# We smooth the output, which is otherwize noisy because of area discretization
df_runoff = df_runoff.rolling(31, center=True, min_periods=1).mean()
fig, ax = plt.subplots(figsize=(10, 3.5), sharex=True)
df_runoff.sum(axis=1).plot(ax=ax);
plt.ylabel('Runoff (Mt)'); plt.xlabel('Years'); plt.title(f'Total annual runoff for {rgi_id}');
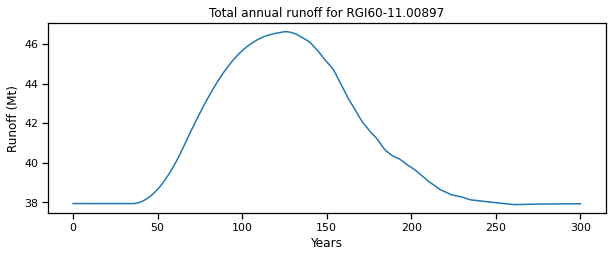
Las variables hidrológicas se calculan sobre la mayor área posible cubierta por hielo glaciar durante la simulación. Esto es equivalente a la escorrentía que se mediría en una estación hidrológica de calibre fijo en el extremo del glaciar. La escorrentía total anual consta de los siguientes componentes:
fusión fuera del glaciar: la nieve se derrite en áreas que ahora están libres de glaciares (es decir, 0 en el año de mayor extensión del glaciar, en este ejemplo al comienzo de la simulación)
derretimiento en el glaciar: hielo + nieve estacional derretida en el glaciar
precipitación líquida dentro y fuera del glaciar (esta última siendo cero en el año de mayor extensión glacial, en este ejemplo al comienzo de la simulación)
f, ax = plt.subplots(figsize=(10, 6));
df_runoff.plot.area(ax=ax, color=sns.color_palette('rocket')); plt.xlabel('Years'); plt.ylabel('Runoff (Mt)'); plt.title(rgi_id);
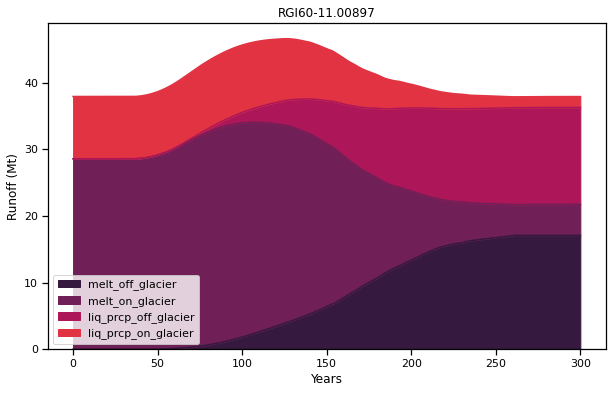
La longitud y el volumen del glaciar disminuyen desde el año 50 en adelante hasta aproximadamente el año 250; esta es la fase de retroceso del glaciar. Posteriormente, la longitud y el volumen se estabilizan en un valor constante, lo que indica que el glaciar ha alcanzado el equilibrio. Ahora estudie el gráfico anterior y sus cuatro componentes principales. Preguntas a abordar:
¿Cuándo se alcanza el “pico de agua”? ¿Tiene esto algo que ver con un cambio en la tendencia de la temperatura en sí? Si no, ¿cuál es la razón por la que se produce el “pico de agua”?
Verifique que la escorrentía total de calibre fijo (¿recuerda lo que esto significa?) sea la misma al principio y al final de la simulación. ¿Por qué es así? ¿Qué cambió en el medio?
La temperatura se estabiliza en el año 200, pero todas las variables hidrológicas continúan cambiando después de eso. ¿Lo que está sucediendo allí?
¿Cuál es la contribución de la precipitación líquida al principio y al final de la simulación? ¿Qué cambió?
¿Puede verificar que la contribución neta del glaciar a la escorrentía (es decir, - \(\Delta M / \Delta t\) es cero al principio y al final de la simulación y positiva en el medio? ¿Por qué esperamos este comportamiento? Sugerencia: compare los resultados con el gráfico de escorrentía idealizado que presentamos al principio de este capítulo
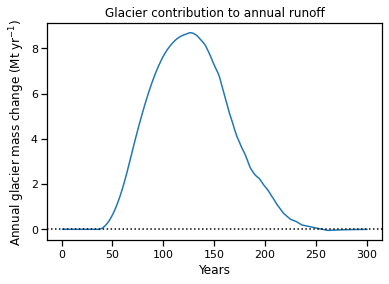
# Solution of the last question above
glacier_mass = ds.volume_m3.to_series() * oggm.cfg.PARAMS['ice_density'] * 1e-9 # In Megatonnes, Mt
glacier_mass = glacier_mass.rolling(31, center=True, min_periods=1).mean()
(- glacier_mass.diff()).plot()
plt.axhline(y=0, color='k', ls=':')
plt.ylabel('Annual glacier mass change (Mt yr$^{-1}$)')
plt.xlabel('Years'); plt.title('Glacier contribution to annual runoff');
escorrentía mensual¶
Las variables “2D” contienen los mismos datos hidrológicos, pero con resolución mensual (dimensiones [time, month]). Por ejemplo, la escorrentía mensual se puede calcular como:
# Select only the runoff variables and convert them to megatonnes (instead of kg)
monthly_runoff = ds['melt_off_glacier_monthly'] + ds['melt_on_glacier_monthly'] + ds['liq_prcp_off_glacier_monthly'] + ds['liq_prcp_on_glacier_monthly']
monthly_runoff = monthly_runoff.rolling(time=31, center=True, min_periods=1).mean() * 1e-9
monthly_runoff.clip(0).plot(cmap='Blues', cbar_kwargs={'label': 'Runoff (Mt)'}); plt.xlabel('Months'); plt.ylabel('Years');

Pero tenga en cuenta, algo está un poco mal con esta trama (algunos de ustedes pueden haber notado: el derretimiento máximo ocurre en otoño, lo cual es inusual): eso se debe a que las coordenadas OGGM son meses hidrológicos; mejoremos esto:
# This should work in both hemispheres maybe?
ds_roll = ds.roll(month_2d=ds['calendar_month_2d'].data[0] - 1, roll_coords=True)
ds_roll['month_2d'] = ds_roll['calendar_month_2d']
# Select only the runoff variables and convert them to megatonnes (instead of kg)
monthly_runoff = ds_roll['melt_off_glacier_monthly'] + ds_roll['melt_on_glacier_monthly'] + ds_roll['liq_prcp_off_glacier_monthly'] + ds_roll['liq_prcp_on_glacier_monthly']
monthly_runoff = monthly_runoff.rolling(time=31, center=True, min_periods=1).mean() * 1e-9
monthly_runoff.clip(0).plot(cmap='Blues', cbar_kwargs={'label': 'Runoff (Mt)'}); plt.xlabel('Months'); plt.ylabel('Years');

Como podemos ver, la escorrentía es aproximadamente cero durante los meses de invierno, mientras que es relativamente alta durante los meses de verano. Ahora comparemos la escorrentía real con la precipitación total sobre la cuenca:
# Compute total precipitation (Snow + Liquid)
tot_precip = ds_roll['liq_prcp_off_glacier_monthly'] + ds_roll['liq_prcp_on_glacier_monthly'] + ds_roll['snowfall_off_glacier_monthly'] + ds_roll['snowfall_on_glacier_monthly']
tot_precip *= 1e-9 # in Mt
# Plot these data at year 0
yr = 0
r = monthly_runoff.sel(time=yr)
p = tot_precip.sel(time=yr)
f, ax = plt.subplots(figsize=(10, 6));
r.plot(ax=ax, color='C3', label='Monthly runoff', linewidth=3);
p.plot(ax=ax, color='C0', label='Monthly precipitation', linewidth=3);
ax.fill_between(r.month_2d, r, p, where=(p >= r), facecolor='C0', interpolate=True, alpha=0.5)
ax.fill_between(r.month_2d, r, p, where=(r > p), facecolor='C3', interpolate=True, alpha=0.5)
plt.ylabel('Mt yr$^{-1}$'); plt.legend(loc='best');
plt.xlabel('Month'); plt.title(f'Total monthly runoff and precipitation at year {yr}');
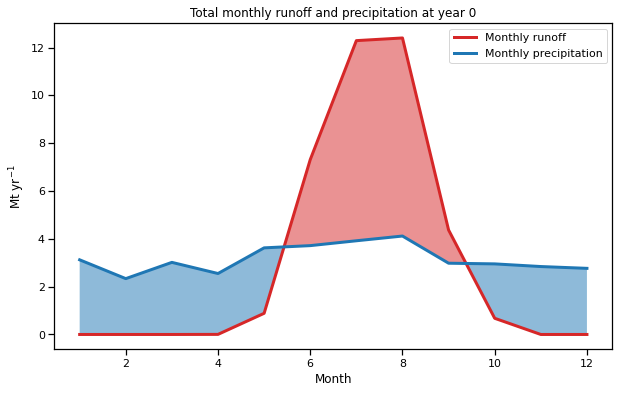
Al comienzo de la simulación, el glaciar está en equilibrio y su contribución anual a la escorrentía es cero. De hecho, esto significa que el área azul en el gráfico de arriba es igual al área roja: la cuenca glaciada libera agua durante el verano, que se acumula en forma de nieve en los meses de invierno. En esta región (Alpes Ötztal, Austria), las precipitaciones son relativamente constantes durante todo el año. Discutir cuáles podrían ser las implicaciones en otros climas del mundo, en particular en climas con una fuerte estacionalidad de las precipitaciones.
Ahora echemos un vistazo al cambio estacional en la escorrentía con el tiempo:
f, ax = plt.subplots(figsize=(10, 6));
cmap = sns.color_palette('magma', 3)
for i, yr in enumerate([0, 120, 300]):
monthly_runoff.sel(time=yr).plot(ax=ax, color=cmap[i], label=f'Year {yr}')
plt.ylabel('Mt yr$^{-1}$'); plt.legend(loc='best');
plt.xlabel('Month'); plt.title('Total monthly runoff change with time');
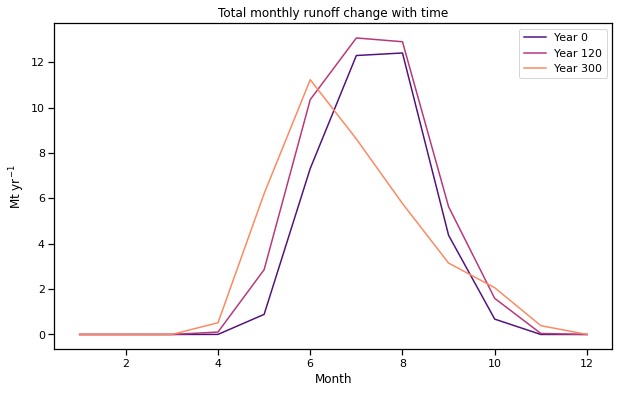
Preguntas para explorar:
verifique que la escorrentía anual sea la misma en el año 0 que en el año 300. ¿Qué cambió en el medio?
¿Cuál es el responsable del cambio de derretimiento de verano a derretimiento de primavera?
¿Cómo cambia la escorrentía en el “pico de agua” (aprox. año 120)?
discutir las implicaciones de este cambio en la estacionalidad para Hintereisferner y para otras regiones del mundo. **Ahora repite este cuaderno (idealmente copiándolo primero) con otras regiones del mundo, donde el clima puede ser muy diferente. ** Tenga en cuenta que nuestras explicaciones son muy específicas del glaciar. Entonces, si cambia el glaciar usando otro rgi_id, ¡es posible que también deba adaptar las explicaciones! ¡También puedes cambiar los parámetros de las simulaciones! ¿Qué sucede cuando el cambio de temperatura es más grande/más rápido, más pequeño/más lento? ¿Cuáles son las implicaciones para el “pico de agua”?
Terminando¶
Ahora concluyamos este cuaderno reproduciendo la famosa trama de Huss & Hock (2018) con nuestros datos.
 Gráfico de Huss & Hock (2018)
Gráfico de Huss & Hock (2018)
# Make a dataframe out of the xarray dataset for simplicity
df_monthly_runoff = pd.DataFrame(monthly_runoff.data, index=ds.time, columns=monthly_runoff.month_2d)
# Create new columns for each season (we define seasons from the perspective of the northern Hemisphere)
df_monthly_runoff['Spring (Apr-Jun)'] = df_monthly_runoff[[4, 5, 6]].sum(axis=1)
df_monthly_runoff['Summer (Jul-Sep)'] = df_monthly_runoff[[7, 8, 9]].sum(axis=1)
df_monthly_runoff['Winter (Oct-Mar)'] = df_monthly_runoff[[10, 11, 12, 1, 2, 3]].sum(axis=1)
df_monthly_runoff.columns.name = 'Season'
# Plot it
# Attention the seasons and labels might need to be adapted if a glacier in a different region is used!
f, ax = plt.subplots(figsize=(10, 6));
df_monthly_runoff[['Spring (Apr-Jun)', 'Summer (Jul-Sep)', 'Winter (Oct-Mar)']].plot.area(ax=ax, color=sns.color_palette('rocket'));
plt.xlabel('Years'); plt.ylabel('Runoff (Mt)'); plt.title('Runoff by season');

Y ahora la trama real:
f, (ax1, ax2) = plt.subplots(2, 1, gridspec_kw={'height_ratios': [2, 1]}, figsize=(10, 8), sharex=True)
p1 = df_monthly_runoff[['Spring (Apr-Jun)', 'Summer (Jul-Sep)', 'Winter (Oct-Mar)']].sum(axis=1)
p2 = df_monthly_runoff['Summer (Jul-Sep)'] # July to September is here the melt season
p1.plot(ax=ax1, color='C0', label='Annual runoff', linewidth=3)
p2.plot(ax=ax1, color='C3', label='Melt-season runoff', linewidth=3);
ax1.hlines([p1.loc[0], p2.loc[0]], 0, 300, color=['C0', 'C3'], linestyle=[':']);
ax1.legend(); ax1.set_xlabel(''); ax1.set_ylabel('Runoff (Mt)');
(temp_bias_ts + 2).plot(ax=ax2, color='C2', label='Temperature', linewidth=3);
ax2.legend(loc='lower right'); ax2.set_xlabel('Years'); ax2.set_ylabel('$\Delta T (°C)$');
sns.despine();
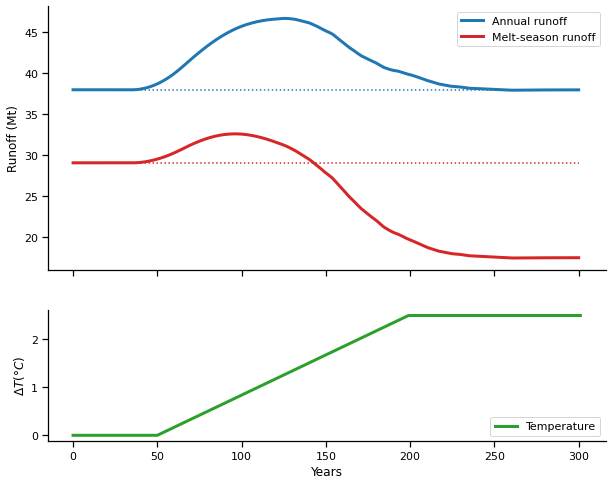
Tenga en cuenta que las dos gráficas anteriores son muy específicas del glaciar. Si usa un glaciar con otro clima, es posible que deba adaptar las gráficas, porque siempre estamos interesados en aquellos meses en los que la escorrentía del glaciar contribuye más a la escorrentía total. Ejemplo dado, para Artesonraju en Perú, estamos más interesados en junio, julio, agosto y septiembre ya que esta es la estación seca, donde casi no llueve.
Llévate puntos a casa¶
Los glaciares en equilibrio no son recursos hídricos netos: ganan tanta masa como liberan
Sin embargo, tienen un papel amortiguador estacional, liberando agua durante los meses de deshielo.
Cuando los glaciares se derriten, se convierten en recursos hídricos netos. El “pico de agua” es el momento en el que el suministro de deshielo de los glaciares alcanza su máximo, es decir, cuando se produce la máxima escorrentía.
Referencias¶
Huss, M. y Hock, R.: Respuesta hidrológica a escala mundial a la futura pérdida de masa de los glaciares, Nat. Clima Chang., 8(2), 135–140, doi:10.1038/s41558-017-0049-x, 2018.
Un recent blog post sobre el papel de los glaciares en el ciclo hidrológico
¿Que sigue?¶
xx_markdown_enlace_xx
