A major objective of the IACS Working Group on Glacier Ice Thickness Estimation is to provide an “estimated ice thickness distribution for every glacier included in the RGI”. After a comparison of ice thickness models for a handful of glaciers (Ice Thickness Models Intercomparison eXperiment, phase 1), the models able to estimate ice thickness on a large number of glaciers with limited input data where invited to participate to the G2TI (see the official announcement here).
A perfect job for OGGM, right? At least this is what I thought one year ago when I pushed Daniel to go on with his plans, right in time for the upcoming IPCC deadlines. As it turns out (I should be used to it by now), the job was harder than I previously thought. Not because OGGM cannot estimate the ice thickness of any glacier (we’ve shown that it can), but because the actual question is how good can OGGM do that? OGGM performed quite favorably in ITMIX 1, but we are playing in another league here.
This document summarizes the major steps undertaken for this goal, and will be concluded by many (many) open questions on how to go forward from here.
Step 1: ingesting G2TI data into OGGM
(spoiler: we failed)
The input data provided for the experiment was, for each glacier:
- the glacier outlines from the RGI version 6
- a local topography map nicely prepared by Matthias
And, for 1087 of them, calibration/validation data in the form of point GPR measurements (808 glaciers) or glacier averaged ice thickness (337). We’ll get back to these later.
OGGM is a standalone tool and doesn’t need this input, but the point of the experiment was to at least agree on something: the topography and the glacier masks. Unfortunately, this didn’t work well for us, for a couple or obstacles which weren’t impossible to tackle but annoying enough for me to avoid them.
First, the provided data wasn’t exactly extracted from RGI Version 6: the outlines
are from the beta version and still have an RGI id version 5. This was a minor
problem, because I just had to replace 50 with 60. I noted some other
differences though: in at least one RGI region (RGI Region 02), the number of
glaciers didn’t match exactly between both versions. So far so good, no big
deal, we can work with that.
Second, Matthias and OGGM of course have different opinions about which resolution is best for the local DEM map. OGGM’s default is to use a square root function of the glacier size:
[\Delta x \textrm{[m]} = a \, \sqrt{\textrm{area} \textrm{[km]}} + b]
with a = 14 and b = 10. When the resolution $\Delta x$ exceeds 200 m, is is caped to that value. This choice wasn’t driven by a real quantitative analysis, I just had a look at a set of glaciers and it looked OK to me. Now let’s compare this to the data provided by Matthias:
So the thing here is that G2TI uses a step function (with steps 25, 50, 100, and 200 m), while OGGM (and this is the most important) is much faster in reaching the 200 m mark. I am not going to argue here which method is best, but what is sure is that because of computational efficiency OGGM cannot really use such high resolution for very large glaciers. Inversely, for very small glaciers (< 1km$^2$), OGGM has a finer resolution than G2TI. Altogether I might have been able to use workarounds (like reprojecting G2TI data into an OGGM map), if it wasn’t for point 3 and 4 below.
Third, OGGM really needs to compute the glacier masks itself. This is currently a limitation in the model, but we need to have glacier geometries and raster witch fit exactly in order to compute the centerlines. So I would’nt have been able to use the G2TI glacier masks anyway.
Fourth, the G2TI data is a “noisy” for resolutions higher that from the original data. It’s not very visible when looking at the DEM itself (left plot below), but it is clear when computing the slope (right plot). For comparison, I plotted the slope computed using a DEM generated on the same map with GDAL.

Again, it’s not a big deal because we smooth the data a lot in OGGM (like all other models do), but all this together summed up to a series of annoyances I didn’t want to deal with. So I decided to use the standard OGGM workflow and reproject everything back to the G2TI map at the very last step.
Step 2: decide how to compute the distributed ice thickness maps
OGGM prime objective is to model glaciers, not to provide distributed ice thickness maps. Similar to Farinotti et al. (2009) and Huss & Farinotti (2012), we have to trick to convert the 1D “flowline” glaciers back to 2D bed topography maps. For ITMIX I coded this part of the model in one afternoon, and I promised myself I was going to try harder for G2TI. In the end, I’m not sure I really managed to do better.
The core of the problem is that this backwards step (from flowline to distributed) is statistical in essence and has very little physical meaning. There are multiple ways to do it, and I tried two major paths:
- handle the computed thickness at the centerline as “true” and interpolating between the centerline points and the glacier boundaries. This works quite well for glaciers where the centerlines are well defined.
- assigning the centerlines thicknesses to the 2D glacier according to elevation bands and adding a scaling factor depending on the distance from the glacier outline. This is more robust for poorly defined centerlines.
Here is an example at the South Glacier (see ITMIX paper for details about the Glacier):
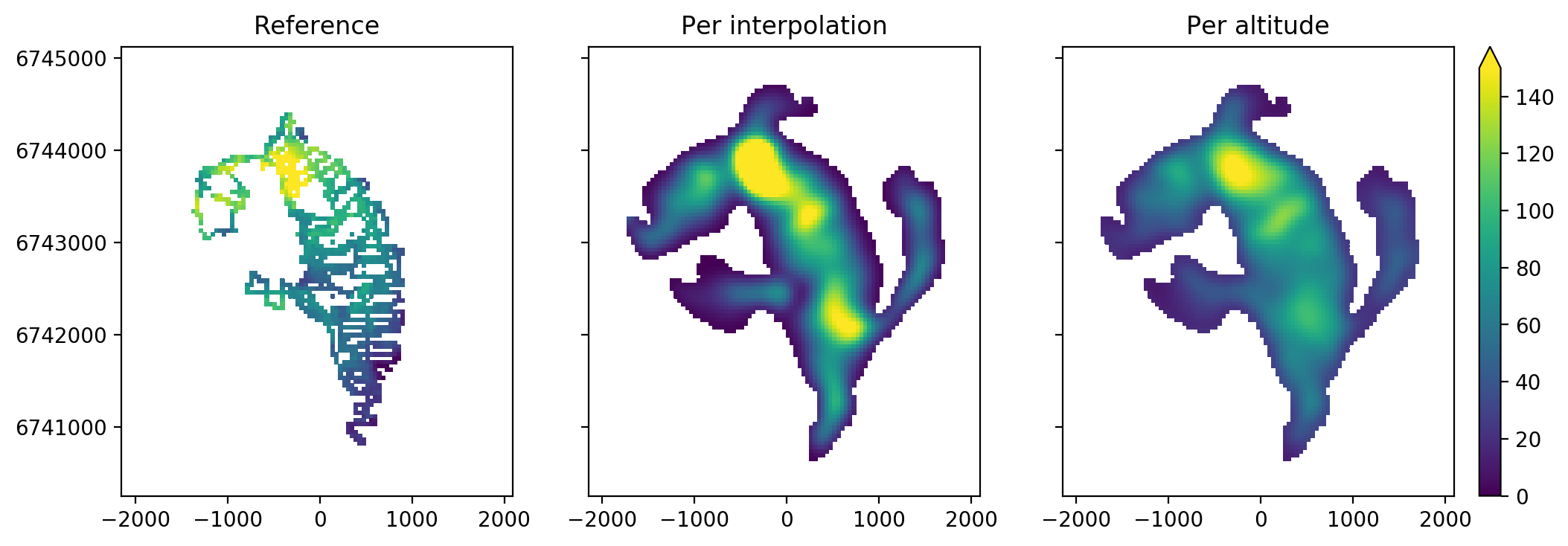
There are quite large differences between the twi methods. In this case (and, as it turns out, in most cases), the altitudinal band method works best. Here is how it really performs in a point scatter-plot:
And this is one of the good examples. There are still obvious problems (like an overestimation close to the glacier boundaries), and it is surely possible to tweak the model towards better results for this one glacier. However, I wanted to work in a much more systematic way.
And here starts the trouble.
I tested a lot of different parameter combinations: for each of the two methods, I varied (i) the influence of the distance to the boundaries, (ii) the radius of the smoothing applied to the final thickness map, and (iii) Glen’s flow law parameter A.
Because this step was about deciding the interpolation parameters only, I made two decisions:
- I manually selected 156 glaciers which I thought had representative GPR data: that is, many points well distributed among the glacier. This makes kind of sense because I didn’t want to take decisions based on a couple of GPR points at the glacier tongue only.
- To remove the effect of systematic bias, I kept only the parameter combinations where the initial calibration of Glen’s A (which controls the average thickness of the glacier) was successful (average bias close to zero).
For example at glacier RGI60-01.16195:
The shape of the curve just shows the different parameter combinations for the two interpolation methods and for increasing A. I colored the selected points based on bias only in green. From these, I selected the best performing with respect to Mean Absolute Deviation (MAD, red).
I repeated this step for all 131 glaciers (156 minus the 25 where the A calibration failed), and finally counted the number of times a certain interpolation strategy would work best. The strategy which performed most often was the altitudinal band method with a smoothing radius of 250 m and a distance to border mask elevated at the power 1/4. These are now the default parameters in OGGM.
Note: I repeated this with the 3-fold cross-validation step imposed by G2TI, and it was always the same strategy which performed best in all cases. Or, I should say, the “less worse”.
Step 3: calibrate Glen’s A
While the interpolation strategy surely plays an important role once the total volume of the glacier is guessed correctly, it is the A calibration step which is extremely difficult to get correctly and has the most influence.
In OGGM we use Glen’s A as calibration parameter for the total glacier volume because it is known to vary between glaciers and because it has a strong influence on glacier volume. It must be noted however that we use it mostly as a tuning parameter, and that its physical meaning should not be over-interpreted.
As a reminder, here is a plot of global glacier volume as a function of a multiplication factor applied to the default Glen parameter A (the plot is from our GMD paper):
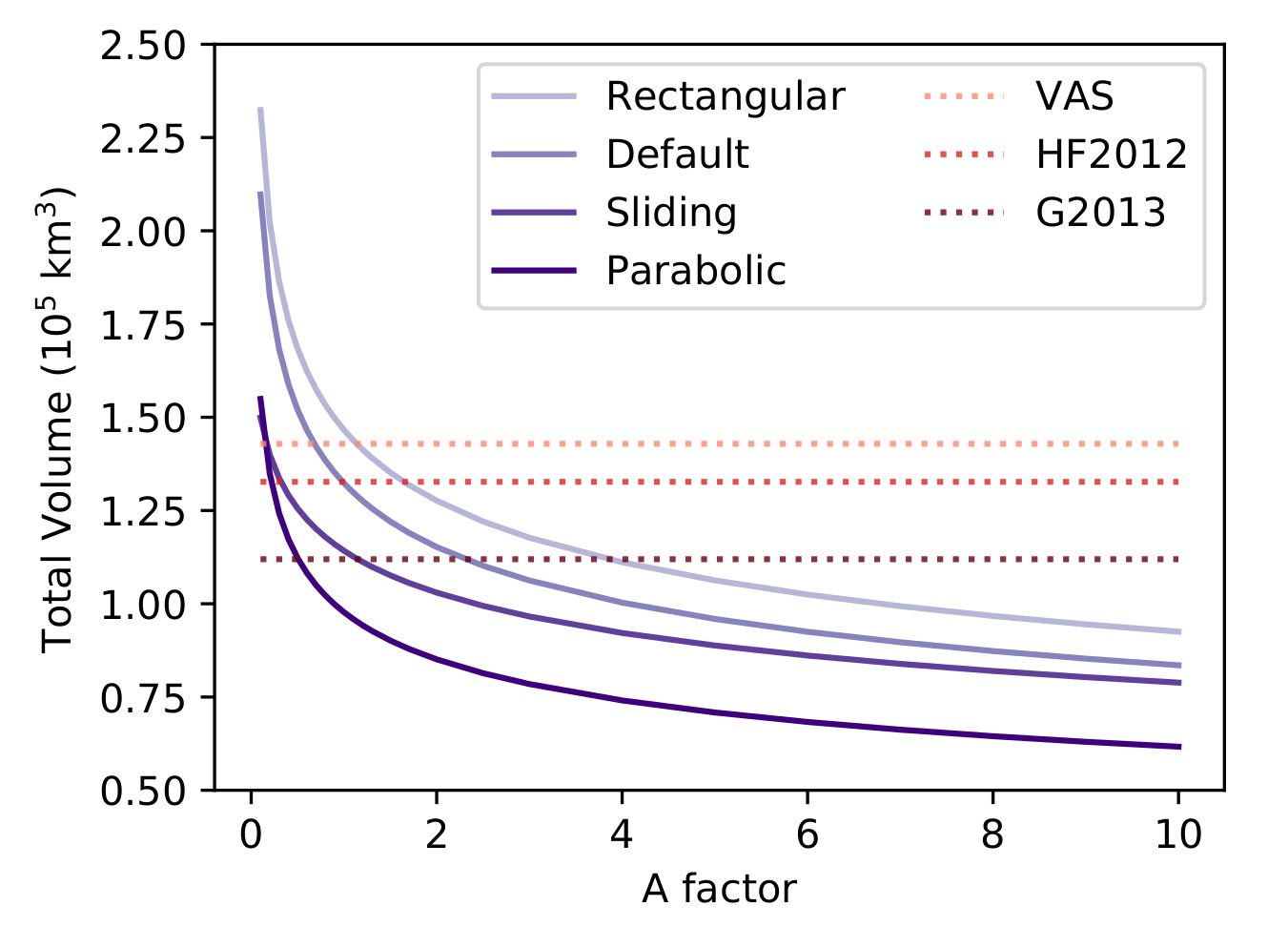
The question I wanted to answer in step 3 is: can we pinpoint A to a certain value so that our global estimates of ice volume are better constrained?
(spoiler: I don’t think I managed, but I did my best in the time that was allocated to me)
Ideal: find a way to calibrate A as a function of <.>
For glaciers with observations, it is possible to tune A so that the bias for this glacier is equal to zero. I tried to plot this “ideal A” as a function of many (many) parameters (e.g. glacier temperature, altitude, location, size…), leading to the production of many (many) clouds of points. Nothing seemed to correlate, with one exception maybe: the plot below shows the “ideal factor” for A as a function of glacier area.
From the plot it looks like smaller glaciers are more likely to be over-estimated than larger glaciers. However, the data is way too uncertain to make significant conclusions.
Less ideal: fix A to a compromise value
Assuming that the glaciers with GPR data are representative for all glaciers worldwide (which they aren’t), let’s just pick an A so that the mean error is minimized for all glaciers. This seems quite simple, but this leads to many new questions without answers:
- should all glaciers have the same weight?
- if not, what is important? Glacier size? Location? Number of GPR points?
- which score do we minimize? MAD? RMSD? BIAS?
Here is an example of the influence of this minimization process applied to different performance measures: average bias, average bias weighted by glacier area, average bias weighted by number of GPR points. We can repeat the operation with MAD, and then another time for the 156 reference glaciers only. This leads to many possible curves to minimize as shown in the plot below. Each vertical black line represents a possible optimum, which are objectively all as valid as the others.
We find a range of “best factors” varying from 1.2 to 2.5. A value higher than unity is physically reasonable to compensate for two model approximations: (i) we neglect basal sliding, and (ii) we assume hat the glacier is in equilibrium. Higher A means higher velocities and thinner glaciers, compensating for both effects.
But, from all these “best” values, which one should we chose?
Pragmatic: just pick one and stop calibrating
My final choice: let’s pick the A factor minimizing the area-weighted average of MAD for the reference glaciers only. This gives us the following results:
- fA = 1.5 for the final run
- fA = 1.7 for the 3-fold cross-validation set 1
- fA = 1.3 for the 3-fold cross-validation set 2
- fA = 1.0 for the 3-fold cross-validation set 3
How bad are we with this setup?
Let’s leave this for Daniel to find out. My gut feeling is not so good: we still have plenty to learn, and I believe that with dedicated research we can improve OGGM a lot.
Step 4: convert OGGM maps back to G2TI
This is quite easy to do. Unfortunately, because of Step 1, our glacier masks and topography do not match exactly the ones provided by G2TI. I hope the G2TI chef will not mind too much…
Step 5: reflect and go forward from here
TODO





