Glacier length changes and initial conditions

Note: this blog post is a work in progress and it might be edited for content from time to time.

The code used to generate the plots available here.

With this short note we illustrate why the non-linear behavior of glaciers make the job of linking climate change to glacier length changes quite a challenging task.

Our study glacier is the Hintereisferner, a medium sized Glacier in the Austrian Alps (according to the model, the glacier in 2003 had a length of approximately 7 km).

Length changes and random climate

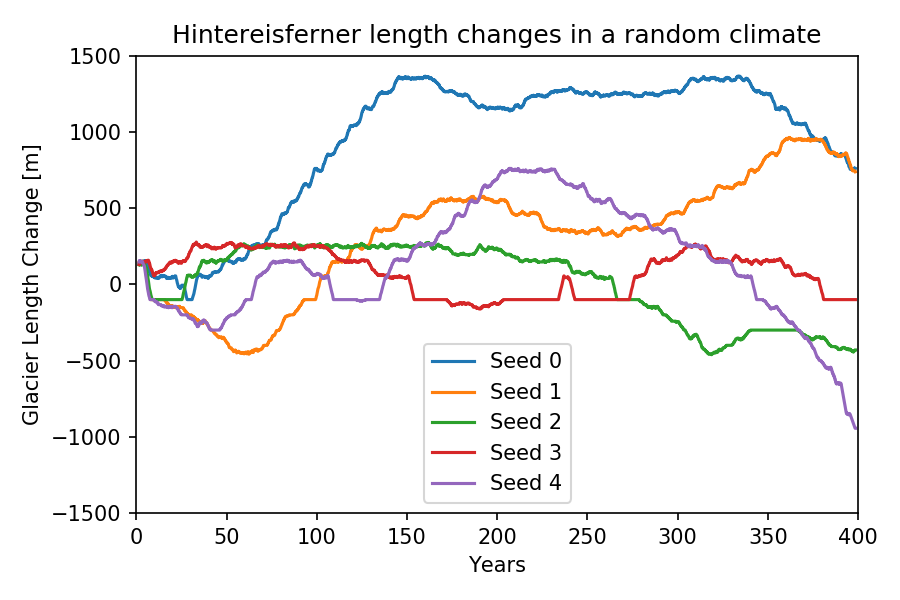
In this first experiment, we run the model under a random climate around the year t$^{*}$ (representing an equilibrium state for the glacier). The random climate is generated simply by shuffling random years of this 31 year period. We do this with 5 different random sequences:

One can see that depending on the climate sequence, absolute length changes of the order of magnitude of kilometers is not unusual. Note that this doesn’t imply that the random climate sequence doesn’t contain a climate variability signal: the random time series indeed include colder and warmer periods, and the glacier responds to them.

Experiment 2: wrong initial state

Now we drive the glacier run with real climate data (obtained from HISTALP) during the period 1855-2003 and we compare the modeled length changes with observations from P. Leclercq’s glacier length fluctuations database.

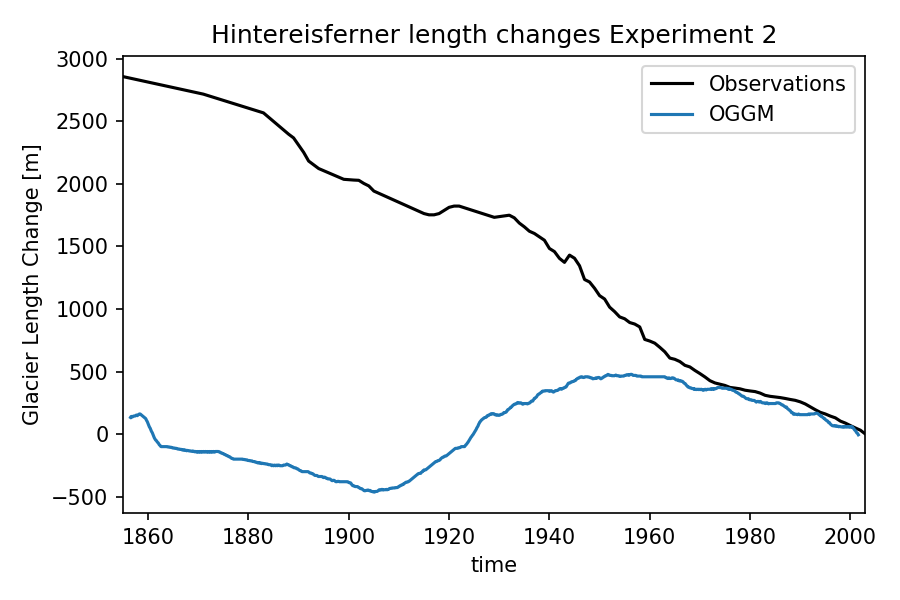
Since we don’t know how the glacier looked like in 1850, we compare the relative length changes only. In this experiment, we initialise the model with today’s glacier geometry. Let’s see what happens:

This result is particularly interesting: if the 1850 Hintereisferner was as big as it is today, it would still be of the same size today. How is this possible? I don’t think this has something to do with a model error, and
there is another simple explanation: today’s Hintereisferner would be too small for the 1900’s climate (i.e. in disequilibrium). As shown by the model output, the glacier grows during the colder first half of the 20th century as a response to it’s small size, and starts to melt again as delayed response to the warming of the second half of the century.

Experiment 3: a better initial state

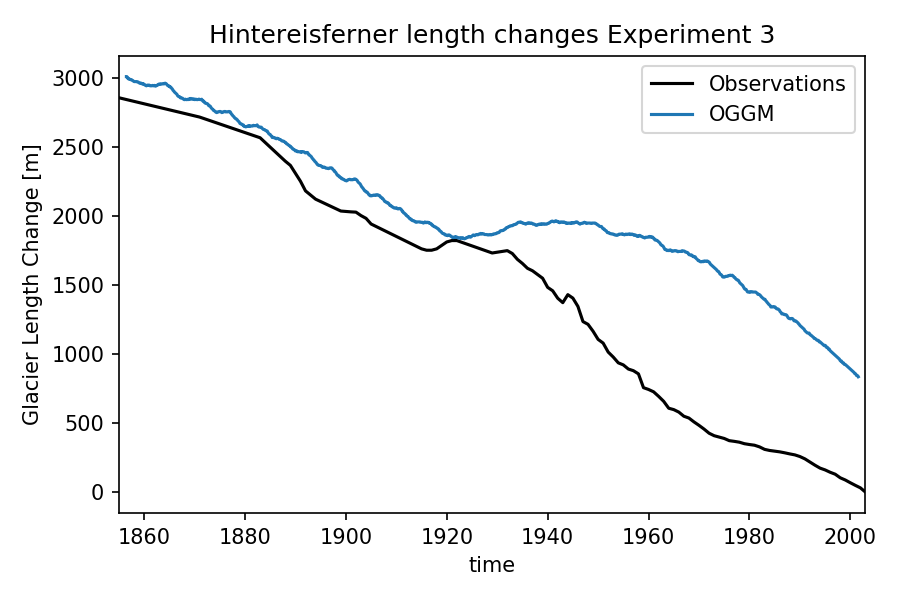
In fact, we know that the glacier was much larger than it is today (about 3 km longer according to observations). With OGGM, we now let the glacier grow under a colder climate¹ and use this larger glacier as initial conditions for our past climate simulation:

This looks much better already. First, the larger glacier is already in disequilibrium with the 1850 climate and therefore shrinks as expected. The shrinkage also stops in the mid-20th century as observed, but the pause is longer (resulting in a 2010 glacier slightly too big in comparison to observations). This could have two reasons: either the glacier response is too slow (pointing towards wrong ice parameters), or the climate forcing is too cold during this period (also plausible).

Experiment 4: a better initial state and other ice parameters

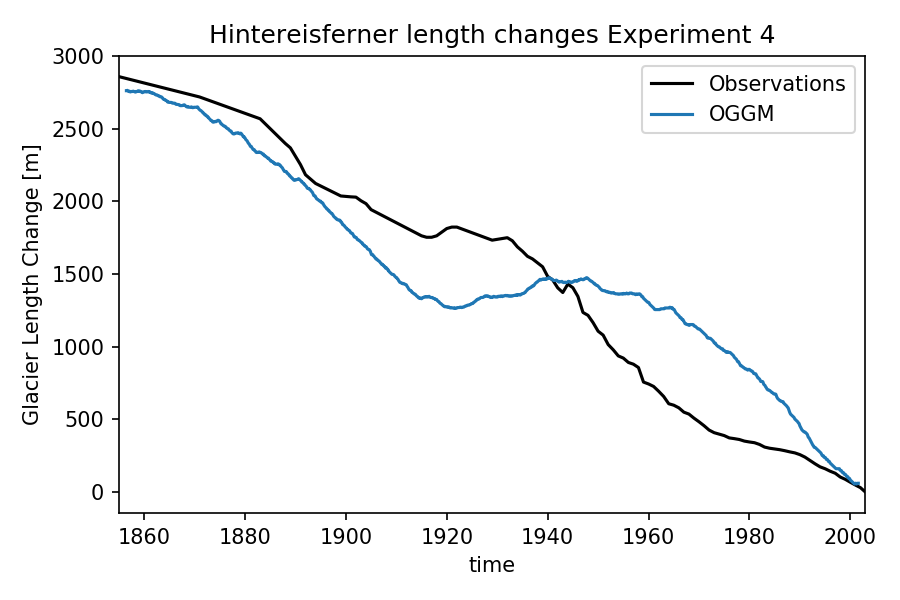
To test the model sensitivity to the ice creep parameter A (see the documentation for more info), we now replicate our experiment but double the values of the ice creep parameter A (this implies a more fluid ice). We grow our glacier to the desired length and run our past model again:

This time, the glacier total response is much closer to expectations, but the response to the 1850-1900 climate is a bit too strong, as is the 1950’s pause. This might be an indication for an inadequate climate forcing.

Preliminary conclusions

If the initial glacier state is known, it is relatively trivial to tune the model for good results (at least in the Hintereisferner case). In a blind run, one can show that unrealistic initial conditions can lead to a plausible present day glacier with a completely wrong path in between (experiment 1).

What do we do from here? The OGGM team members are now working hard on this issue, and are exploring several ways to go forward. In a first step, we are likely to adopt a stochastic approach in which many possible initial states are tested and selected based on the model response.

Addendum

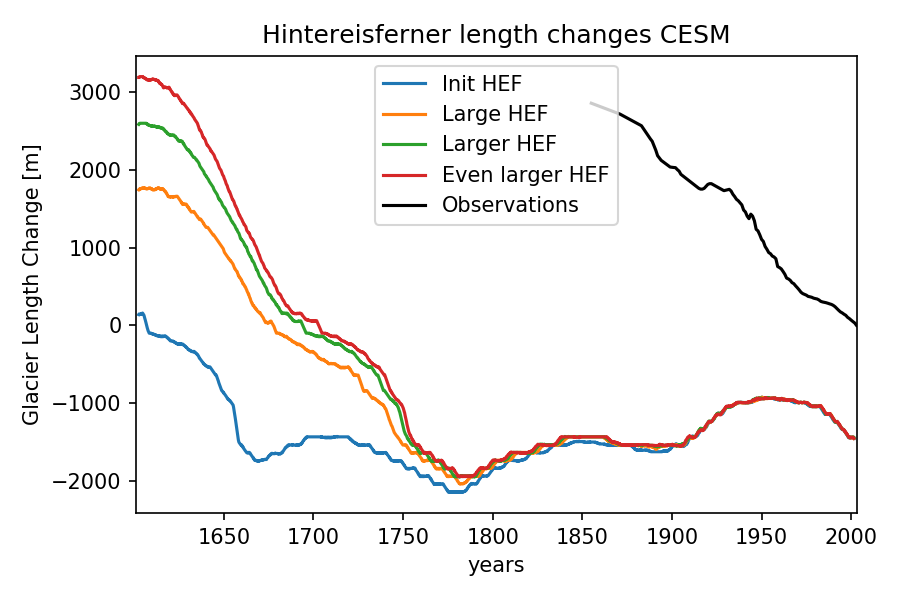
We have shown that the initial glacier state is important for length changes. But how long is the initial state influencing the glacier behavior in a given climate? The answer will depend on the size of the glacier, but for Hintereisferner we can run a simple experiment again: we let the glacier grow at various sizes and then run the model with past climate simulations from the CESM model. The climate forcing is therefore the same for all simulations (from 1600 to 2003):

The good news is that the initial state has a visible influence during the first 150 years or so. This indicates that climate is the most important driver of length changes at long time scales (in particular in this shrinking case). The bad news is, the CESM data seem to be too warm for most of the period and shows a very small Little Ice Age signal.

Notes

---

• ← Previous Post
• Next Post →