Glaciers as water resources: part 2 (projections)#
Goals of this notebook:
run simulations using climate projections to explore the role of glaciers as water resources
Setting the scene: glacier runoff and “peak water”#
We strongly recommend to run Part 1 of this notebook before going on!
Setup#
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context('notebook')
import xarray as xr
import salem
import numpy as np
import pandas as pd
import oggm.cfg
from oggm import utils, workflow, tasks, graphics
# OGGM options
oggm.cfg.initialize(logging_level='WARNING')
oggm.cfg.PATHS['working_dir'] = utils.gettempdir(dirname='WaterResources-Proj')
oggm.cfg.PARAMS['min_ice_thick_for_length'] = 1 # a glacier is when ice thicker than 1m
oggm.cfg.PARAMS['store_model_geometry'] = True
2023-03-23 08:43:33: oggm.cfg: Reading default parameters from the OGGM `params.cfg` configuration file.
2023-03-23 08:43:33: oggm.cfg: Multiprocessing switched OFF according to the parameter file.
2023-03-23 08:43:33: oggm.cfg: Multiprocessing: using all available processors (N=8)
2023-03-23 08:43:33: oggm.cfg: PARAMS['min_ice_thick_for_length'] changed from `0.0` to `1`.
2023-03-23 08:43:33: oggm.cfg: PARAMS['store_model_geometry'] changed from `False` to `True`.
Define the glacier we will play with#
For this notebook we use the Hintereisferner, Austria. Some other possibilities to play with:
Hintereisferner, Austria: RGI60-11.00897
Artesonraju, Peru: RGI60-16.02444
Rikha Samba, Nepal: RGI60-15.04847
Parlung No. 94, China: RGI60-15.11693
And virtually any glacier you can find the RGI Id from, e.g. in the GLIMS viewer! Large glaciers may need longer simulations to see changes though. For less uncertain calibration parameters, we also recommend to pick one of the many reference glaciers in this list, where we make sure that observations of mass-balance are better matched.
Let’s start with Hintereisferner first and you’ll be invited to try out your favorite glacier at the end of this notebook.
# Hintereisferner
rgi_id = 'RGI60-11.00897'
Preparing the glacier data#
This can take up to a few minutes on the first call because of the download of the required data:
# We pick the elevation-bands glaciers because they run a bit faster - but they create more step changes in the area outputs
base_url = 'https://cluster.klima.uni-bremen.de/~oggm/gdirs/oggm_v1.6/L3-L5_files/2023.1/elev_bands/W5E5_spinup'
gdir = workflow.init_glacier_directories([rgi_id], from_prepro_level=5, prepro_border=160, prepro_base_url=base_url)[0]
2023-03-23 08:43:33: oggm.workflow: init_glacier_directories from prepro level 5 on 1 glaciers.
2023-03-23 08:43:33: oggm.workflow: Execute entity tasks [gdir_from_prepro] on 1 glaciers
Interactive glacier map#
A first glimpse on the glacier of interest.
Tip: You can use the mouse to pan and zoom in the map
# One interactive plot below requires Bokeh
# The rest of the notebook works without this dependency - comment if needed
import holoviews as hv
hv.extension('bokeh')
import geoviews as gv
import geoviews.tile_sources as gts
sh = salem.transform_geopandas(gdir.read_shapefile('outlines'))
(gv.Polygons(sh).opts(fill_color=None, color_index=None) *
gts.tile_sources['EsriImagery'] * gts.tile_sources['StamenLabels']).opts(width=750, height=500, active_tools=['pan', 'wheel_zoom'])
Past run#
The glacier directories we are using come with a run called a “spinup”, which is a simulation running from 1980 to 2020 while appoximately matching glacier volume and area at the glacier outline date:
with xr.open_dataset(gdir.get_filepath('model_diagnostics', filesuffix='_spinup_historical')) as ds:
ds = ds.sel(time=slice(2000, 2020)).load()
fig, axs = plt.subplots(nrows=2, figsize=(10, 7), sharex=True)
ds.volume_m3.plot(ax=axs[0]);
ds.area_m2.plot(ax=axs[1]);
axs[1].scatter(gdir.rgi_date+1, gdir.rgi_area_m2, label=f'Glacier area in {gdir.rgi_date+1}');
axs[0].set_xlabel(''); axs[0].set_title(f'{rgi_id}'); axs[1].set_xlabel('Years'); plt.legend();
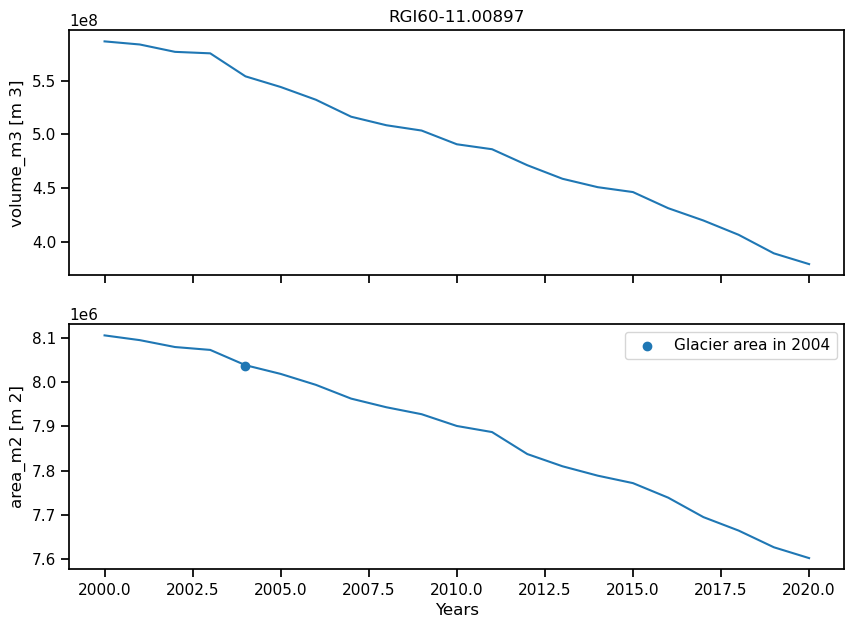
From now on we will use the glacier area and volume as of 2020 to start our simulations.
“Commitment run”#
We are now ready to run our first simulation. This is a so called “commitment run”: how much ice loss is “already committed” for this glacier, even if climate change would stop today? This is a useful but purely theoretical experiment: climate change won’t stop today, unfortunately. To learn more about committed mass-loss at the global scale, read Marzeion et al., 2018.
Here, we run a simulation for 100 years with a constant climate based on the last 11 years:
# file identifier where the model output is saved
file_id = '_ct'
# We are using the task run_with_hydro to store hydrological outputs along with the usual glaciological outputs
tasks.run_with_hydro(gdir,
run_task=tasks.run_constant_climate, # which climate? See below for other examples
nyears=100, # length of the simulation
y0=2014, halfsize=5, # For the constant climate, period over which the climate is taken from
init_model_filesuffix='_spinup_historical', # Start from the glacier in 2020 afer spinup
store_monthly_hydro=True, # Monthly ouptuts provide additional information
output_filesuffix=file_id); # an identifier for the output file to read it later
Then we can take a look at the output:
with xr.open_dataset(gdir.get_filepath('model_diagnostics', filesuffix=file_id)) as ds:
# The last step of hydrological output is NaN (we can't compute it for this year)
ds = ds.isel(time=slice(0, -1)).load()
There are plenty of variables in this dataset! We can list them with:
ds
<xarray.Dataset>
Dimensions: (time: 100, month_2d: 12)
Coordinates:
* time (time) float64 0.0 1.0 2.0 ... 97.0 98.0 99.0
calendar_year (time) int64 0 1 2 3 4 5 ... 94 95 96 97 98 99
calendar_month (time) int64 1 1 1 1 1 1 1 1 ... 1 1 1 1 1 1 1
hydro_year (time) int64 0 1 2 3 4 5 ... 94 95 96 97 98 99
hydro_month (time) int64 4 4 4 4 4 4 4 4 ... 4 4 4 4 4 4 4
* month_2d (month_2d) int64 1 2 3 4 5 6 7 8 9 10 11 12
hydro_month_2d (month_2d) int64 4 5 6 7 8 9 10 11 12 1 2 3
calendar_month_2d (month_2d) int64 1 2 3 4 5 6 7 8 9 10 11 12
Data variables: (12/23)
volume_m3 (time) float64 3.79e+08 ... 1.117e+08
volume_m3_min_h (time) float64 3.79e+08 ... 1.078e+08
volume_bsl_m3 (time) float64 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0
volume_bwl_m3 (time) float64 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0
area_m2 (time) float64 7.602e+06 7.56e+06 ... 3.34e+06
area_m2_min_h (time) float64 7.588e+06 ... 2.932e+06
... ...
liq_prcp_on_glacier (time) float64 9.029e+09 ... 3.161e+09
liq_prcp_on_glacier_monthly (time, month_2d) float64 0.0 0.0 ... 0.0 0.0
snowfall_off_glacier (time) float64 1.544e+06 ... 6.287e+09
snowfall_off_glacier_monthly (time, month_2d) float64 1.345e+05 ... 7.62...
snowfall_on_glacier (time) float64 1.316e+10 ... 6.588e+09
snowfall_on_glacier_monthly (time, month_2d) float64 1.526e+09 ... 5.97...
Attributes:
description: OGGM model output
oggm_version: 1.5.4.dev30+gcd86bbe.d20220905
calendar: 365-day no leap
creation_date: 2023-03-23 07:43:40
water_level: 0
glen_a: 6.0855911376708154e-24
fs: 0
mb_model_class: MultipleFlowlineMassBalance
mb_model_hemisphere: nhTip: you can click on a variable and show it’s attribute with the “page” button on the right.
The time and month_2d variables are coordinates, and the other variables are either provided as additional information (e.g. calendar_month, we will get back to this), or they are providing the actual data. For instance, we can plot the annual evolution of the volume and length of our glacier:
fig, axs = plt.subplots(nrows=2, figsize=(10, 7), sharex=True)
ds.volume_m3.plot(ax=axs[0]);
ds.area_m2.plot(ax=axs[1]);
axs[0].set_xlabel(''); axs[0].set_title(f'{rgi_id}'); axs[1].set_xlabel('Years');
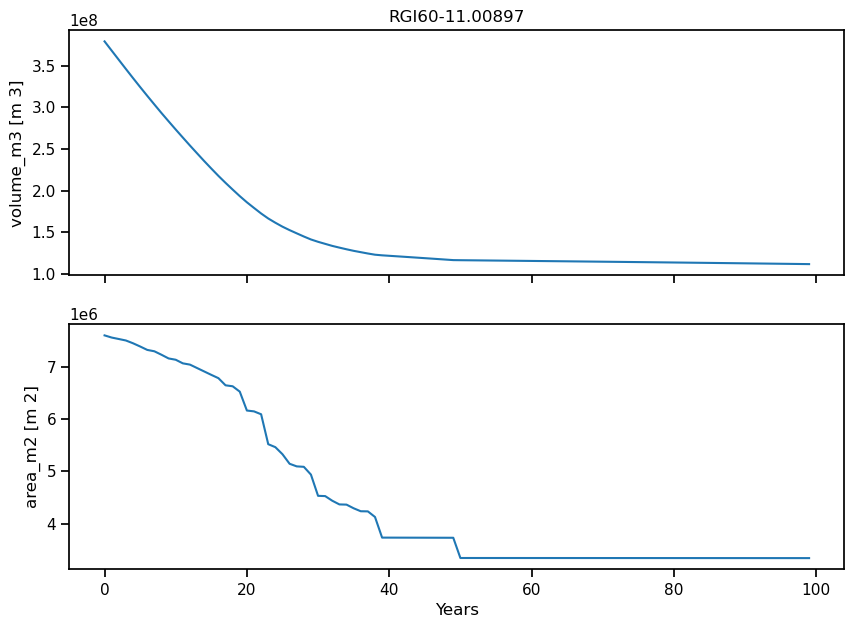
The glacier length and volume decrease during the first ~40 years of the simulation - this is the glacier retreat phase. Afterwards, both length and volume oscillate around a more or less constant value indicating that the glacier has reached equilibrium. The difference between the starting volume and the equilibrium volume is called the committed mass loss. It can be quite high in the Alps, and depends on many factors (such as glacier size, location, and the reference climate period),
Annual runoff#
As glaciers retreat, they contribute to sea-level rise (visit the World Glaciers Explorer OGGM-Edu app for more information!). This is not what we are interested in here. Indeed, they will also have important local impacts: in this notebook, we will have a look at their impact on streamflow.
Let’s take a look at some of the hydrological outputs computed by OGGM. We start by creating a pandas DataFrame of all “1D” (annual) variables:
sel_vars = [v for v in ds.variables if 'month_2d' not in ds[v].dims]
df_annual = ds[sel_vars].to_dataframe()
Then we can select the hydrological varialbes and sum them to get the total annual runoff:
# Select only the runoff variables
runoff_vars = ['melt_off_glacier', 'melt_on_glacier', 'liq_prcp_off_glacier', 'liq_prcp_on_glacier']
# Convert them to megatonnes (instead of kg)
df_runoff = df_annual[runoff_vars] * 1e-9
fig, ax = plt.subplots(figsize=(10, 3.5), sharex=True)
df_runoff.sum(axis=1).plot(ax=ax);
plt.ylabel('Mt'); plt.xlabel('Years'); plt.title(f'Total annual runoff for {rgi_id}');
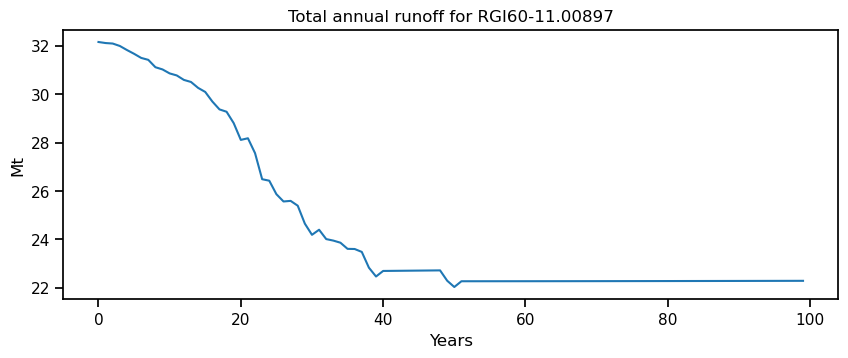
The hydrological variables are computed on the largest possible area that was covered by glacier ice during the simulation. This is equivalent to the runoff that would be measured at a fixed-gauge hydrological station at the glacier terminus.
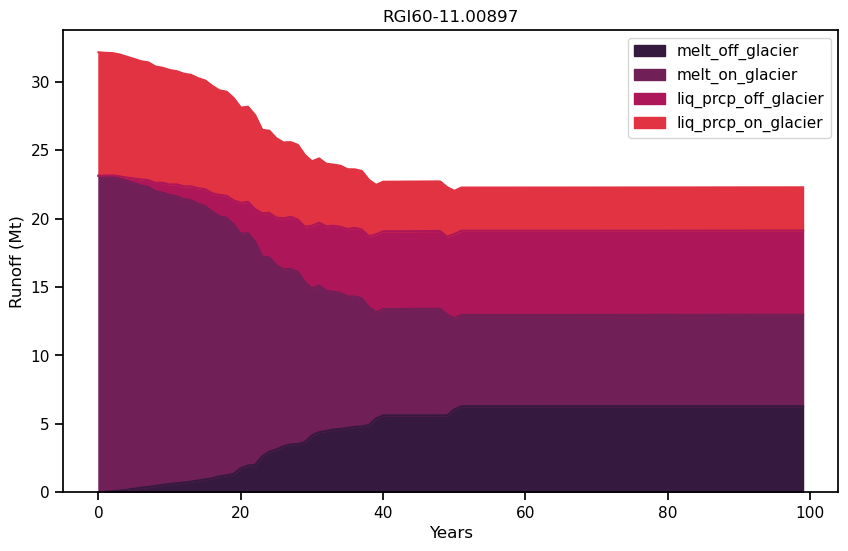
The total annual runoff consists of the following components:
melt off-glacier: snow melt on areas that are now glacier free (i.e. 0 in the year of largest glacier extent, in this example at the start of the simulation)
melt on-glacier: ice + seasonal snow melt on the glacier
liquid precipitaton on- and off-glacier (the latter being zero at the year of largest glacial extent, in this example at start of the simulation)
f, ax = plt.subplots(figsize=(10, 6));
df_runoff.plot.area(ax=ax, color=sns.color_palette("rocket")); plt.xlabel('Years'); plt.ylabel('Runoff (Mt)'); plt.title(rgi_id);
Before we continue, let’s remember ourselves the expected contribution of glaciers to runoff.
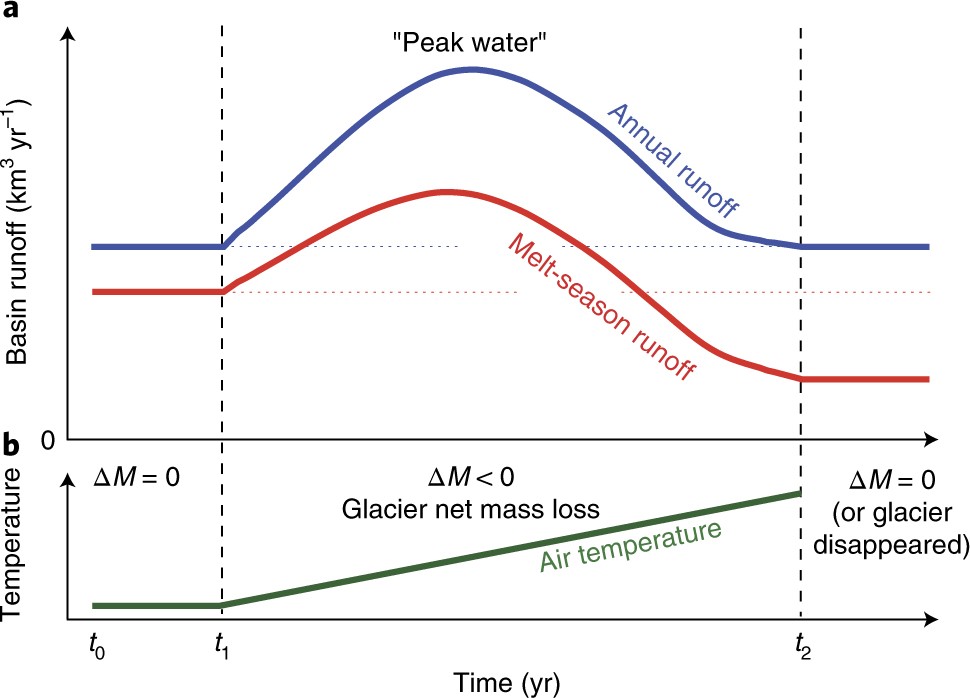
Graphic from Huss & Hock (2018)
Questions to explore:
where approximately on this graph is the studied glacier?
can you explain the relative contribution of each component, based on the previous notebook?
The total runoff out of a glacier basin is the sum of the four contributions above. To show that the glacier total contribution is indeed zero (\(\Delta M = 0\)) when in equilibrium, we can compute it from the glacier mass change:
glacier_mass = ds.volume_m3.to_series() * oggm.cfg.PARAMS['ice_density'] * 1e-9 # In Megatonnes, Mt
glacier_mass.diff().plot()
plt.axhline(y=0, color='k', ls=':')
plt.ylabel('Annual glacier mass change (Mt yr$^{-1}$)')
plt.xlabel('Years'); plt.title('Glacier contribution to annual runoff');
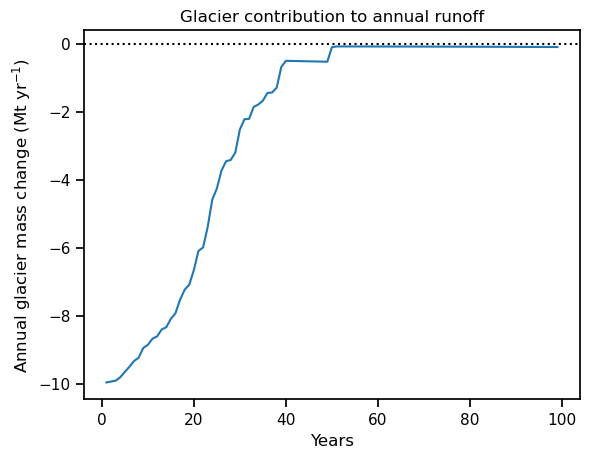
Note that this doesn’t mean that ice is not melting! At equilibrium, this means that the ice that melts each year over the glacier is replaced by snowfall in the accumulation area of the glacier. This illustrates well that glaciers in equilibrium are not net water resources on the annual average: in the course of the year they gain as much mass as they release.
Monthly runoff#
The “2D” variables contain the same data but at monthly resolution, with the dimension (time, month). For example, runoff can be computed the same way:
# Select only the runoff variables and convert them to megatonnes (instead of kg)
monthly_runoff = (ds['melt_off_glacier_monthly'] + ds['melt_on_glacier_monthly'] +
ds['liq_prcp_off_glacier_monthly'] + ds['liq_prcp_on_glacier_monthly'])
monthly_runoff *= 1e-9
monthly_runoff.clip(0).plot(cmap='Blues', cbar_kwargs={'label': 'Mt'}); plt.xlabel('Months'); plt.ylabel('Years');
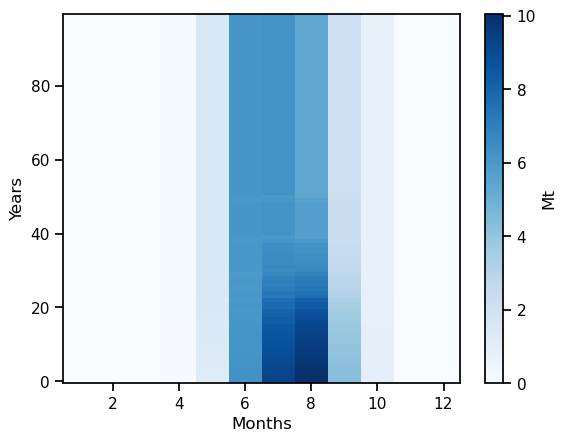
As we can see, the runoff is approximately zero during the winter months, while relatively high during the summer months. This implies that the glacier is a source of water in the summer when it releases the water accumulated in the winter.
The annual cycle changes as the glacier retreats:
monthly_runoff.sel(time=[0, 30, 99]).plot(hue='time');
plt.title('Annual cycle');
plt.xlabel('Month');
plt.ylabel('Runoff (Mt)');
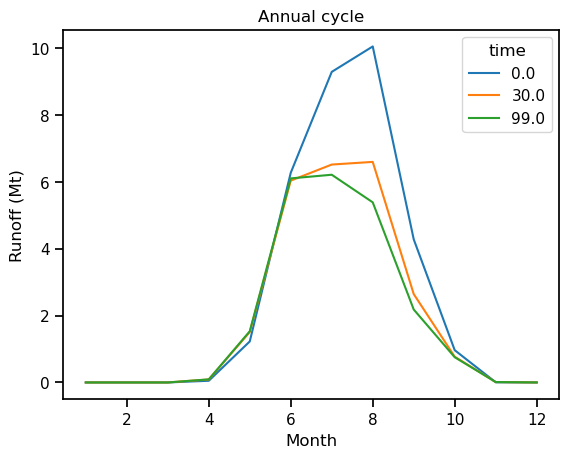
Not only does the total runoff during the summer months decrease as the simulation progresses, the month of maximum runoff is also shifted to earlier in the summer.
21st century projection runs#
You have now learned how to simulate and analyse a specific glacier under a constant climate. We will now take this a step further and simulate two different glaciers, located in different climatic regions, forced with CMIP5 climate projections.
We begin by initializing the glacier directories:
# We keep Hintereisferner from earlier, but also add a new glacier
rgi_ids = [rgi_id, 'RGI60-14.23809']
gdirs = workflow.init_glacier_directories(rgi_ids, from_prepro_level=5, prepro_border=160, prepro_base_url=base_url)
2023-03-23 08:43:44: oggm.workflow: init_glacier_directories from prepro level 5 on 2 glaciers.
2023-03-23 08:43:44: oggm.workflow: Execute entity tasks [gdir_from_prepro] on 2 glaciers
gdirs now contain two glaciers, one in Central Europe and one in the Himalayas:
gdirs
[<oggm.GlacierDirectory>
RGI id: RGI60-11.00897
Region: 11: Central Europe
Subregion: 11-01: Alps
Name: Hintereisferner
Glacier type: Glacier
Terminus type: Land-terminating
Status: Glacier or ice cap
Area: 8.036 km2
Lon, Lat: (10.7584, 46.8003)
Grid (nx, ny): (439, 394)
Grid (dx, dy): (50.0, -50.0),
<oggm.GlacierDirectory>
RGI id: RGI60-14.23809
Region: 14: South Asia West
Subregion: 14-01: Hindu Kush
Glacier type: Glacier
Terminus type: Land-terminating
Status: Glacier or ice cap
Area: 7.4 km2
Lon, Lat: (71.879164896, 36.592710667)
Grid (nx, ny): (403, 403)
Grid (dx, dy): (48.0, -48.0)]
We can take a quick look at the new glacier:
sh = salem.transform_geopandas(gdirs[1].read_shapefile('outlines'))
(gv.Polygons(sh).opts(fill_color=None, color_index=None) *
gts.tile_sources['EsriImagery'] * gts.tile_sources['StamenLabels']).opts(width=750, height=500, active_tools=['pan', 'wheel_zoom'])
Zoom out of the map to find out where the glacier is! Discuss its relevance for water resources.
Climate projections data#
Before we run our future simulation we have to process the climate data for the glacier. We are using the bias-corrected projections from the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP). They are offering climate projections from CMIP6 (the basis for the IPCC AR6) but already bias-corrected to our glacier grid point. Let’s download them:
# you can choose one of these 5 different GCMs:
# 'gfdl-esm4_r1i1p1f1', 'mpi-esm1-2-hr_r1i1p1f1', 'mri-esm2-0_r1i1p1f1' ("low sensitivity" models, within typical ranges from AR6)
# 'ipsl-cm6a-lr_r1i1p1f1', 'ukesm1-0-ll_r1i1p1f2' ("hotter" models, especially ukesm1-0-ll)
from oggm.shop import gcm_climate
member = 'mri-esm2-0_r1i1p1f1'
# Download the three main SSPs
for ssp in ['ssp126', 'ssp370','ssp585']:
# bias correct them
workflow.execute_entity_task(gcm_climate.process_monthly_isimip_data, gdirs,
ssp = ssp,
# gcm member -> you can choose another one
member=member,
# recognize the climate file for later
output_filesuffix=f'_ISIMIP3b_{member}_{ssp}'
);
2023-03-23 08:43:46: oggm.workflow: Execute entity tasks [process_monthly_isimip_data] on 2 glaciers
2023-03-23 08:43:48: oggm.workflow: Execute entity tasks [process_monthly_isimip_data] on 2 glaciers
2023-03-23 08:43:50: oggm.workflow: Execute entity tasks [process_monthly_isimip_data] on 2 glaciers
If you are unfamiliar with CMIP6 and SSPs, spend some time reading about them. What do the ‘ssp126’, ‘ssp370’,’ssp585’ scenarios represent?
Projection run#
With the climate data download complete, we can run the forced simulations:
for ssp in ['ssp126', 'ssp370', 'ssp585']:
rid = f'_ISIMIP3b_{member}_{ssp}'
workflow.execute_entity_task(tasks.run_with_hydro, gdirs,
run_task=tasks.run_from_climate_data, ys=2020,
# use gcm_data, not climate_historical
climate_filename='gcm_data',
# use the chosen scenario
climate_input_filesuffix=rid,
# this is important! Start from 2020 glacier
init_model_filesuffix='_spinup_historical',
# recognize the run for later
output_filesuffix=rid,
# add monthly diagnostics
store_monthly_hydro=True);
2023-03-23 08:43:53: oggm.workflow: Execute entity tasks [run_with_hydro] on 2 glaciers
2023-03-23 08:43:54: oggm.workflow: Execute entity tasks [run_with_hydro] on 2 glaciers
2023-03-23 08:43:55: oggm.workflow: Execute entity tasks [run_with_hydro] on 2 glaciers
# Create the figure
f, ax = plt.subplots(figsize=(18, 7), sharex=True)
# Loop over all scenarios
for i, ssp in enumerate(['ssp126', 'ssp370', 'ssp585']):
file_id = f'_ISIMIP3b_{member}_{ssp}'
# Open the data, gdirs[0] correspond to Hintereisferner.
with xr.open_dataset(gdirs[0].get_filepath('model_diagnostics', filesuffix=file_id)) as ds:
# Load the data into a dataframe
ds = ds.isel(time=slice(0, -1)).load()
# Select annual variables
sel_vars = [v for v in ds.variables if 'month_2d' not in ds[v].dims]
# And create a dataframe
df_annual = ds[sel_vars].to_dataframe()
# Select the variables relevant for runoff.
runoff_vars = ['melt_off_glacier', 'melt_on_glacier', 'liq_prcp_off_glacier', 'liq_prcp_on_glacier']
# Convert to mega tonnes instead of kg.
df_runoff = df_annual[runoff_vars].clip(0) * 1e-9
# Sum the variables each year "axis=1", take the 11 year rolling mean and plot it.
df_roll = df_runoff.sum(axis=1).rolling(window=11, center=True).mean()
df_roll.plot(ax=ax, label=ssp, color=sns.color_palette("rocket")[i])
ax.set_ylabel('Annual runoff (Mt)'); ax.set_xlabel('Year'); plt.title(gdirs[0].rgi_id); plt.legend();
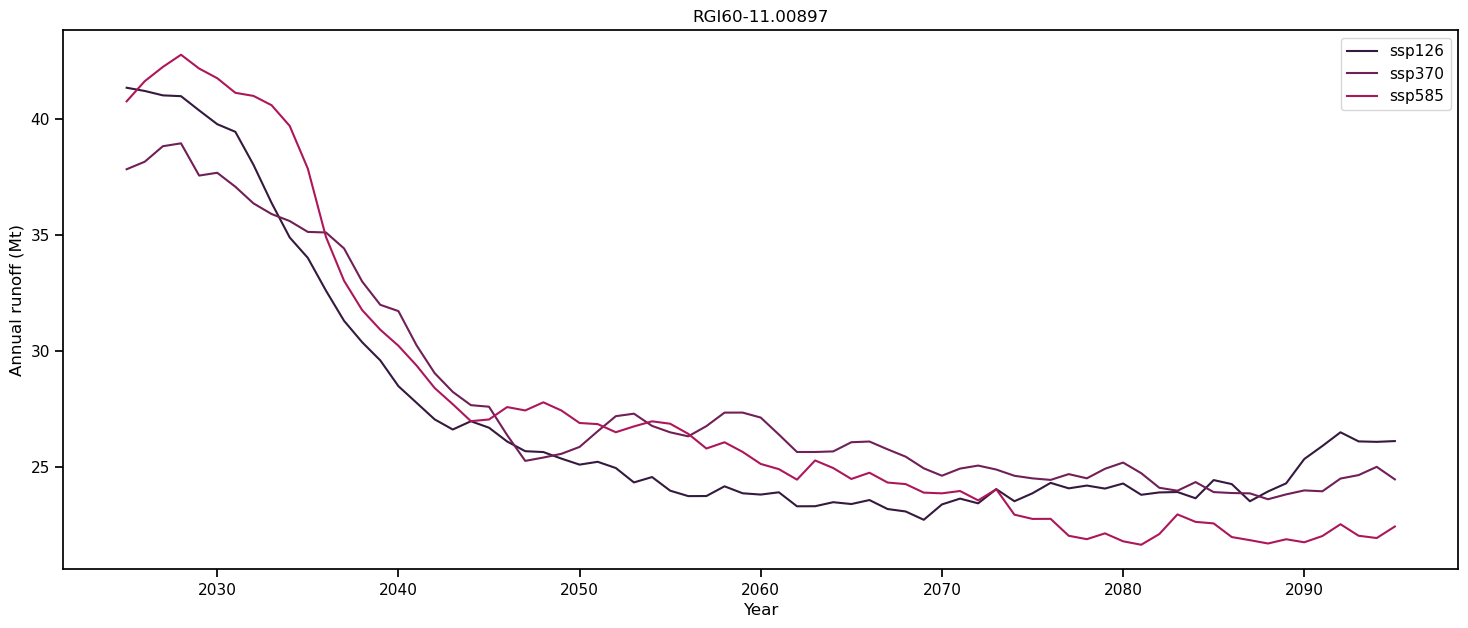
For Hintereisferner, runoff decreases throughout the 21st-century for all scenarios, indicating that peak water has already been reached sometime in the past or is very close to be reached. This is the case for many European glaciers. What about our unnamed glacier in the Himalayas?
# Create the figure
f, ax = plt.subplots(figsize=(18, 7), sharex=True)
# Loop over all scenarios
for i, ssp in enumerate(['ssp126', 'ssp370', 'ssp585']):
file_id = f'_ISIMIP3b_{member}_{ssp}'
# Open the data, gdirs[1] correspond to the unnamed glacier.
with xr.open_dataset(gdirs[1].get_filepath('model_diagnostics', filesuffix=file_id)) as ds:
# Load the data into a dataframe
ds = ds.isel(time=slice(0, -1)).load()
# Select annual variables
sel_vars = [v for v in ds.variables if 'month_2d' not in ds[v].dims]
# And create a dataframe
df_annual = ds[sel_vars].to_dataframe()
# Select the variables relevant for runoff.
runoff_vars = ['melt_off_glacier', 'melt_on_glacier',
'liq_prcp_off_glacier', 'liq_prcp_on_glacier']
# Convert to mega tonnes instead of kg.
df_runoff = df_annual[runoff_vars].clip(0) * 1e-9
# Sum the variables each year "axis=1", take the 11 year rolling mean and plot it.
df_roll = df_runoff.sum(axis=1).rolling(window=11, center=True).mean()
df_roll.plot(ax=ax, label=ssp, color=sns.color_palette("rocket")[i])
ax.set_ylabel('Annual runoff (Mt)'); ax.set_xlabel('Year'); plt.title(gdirs[1].rgi_id); plt.legend();
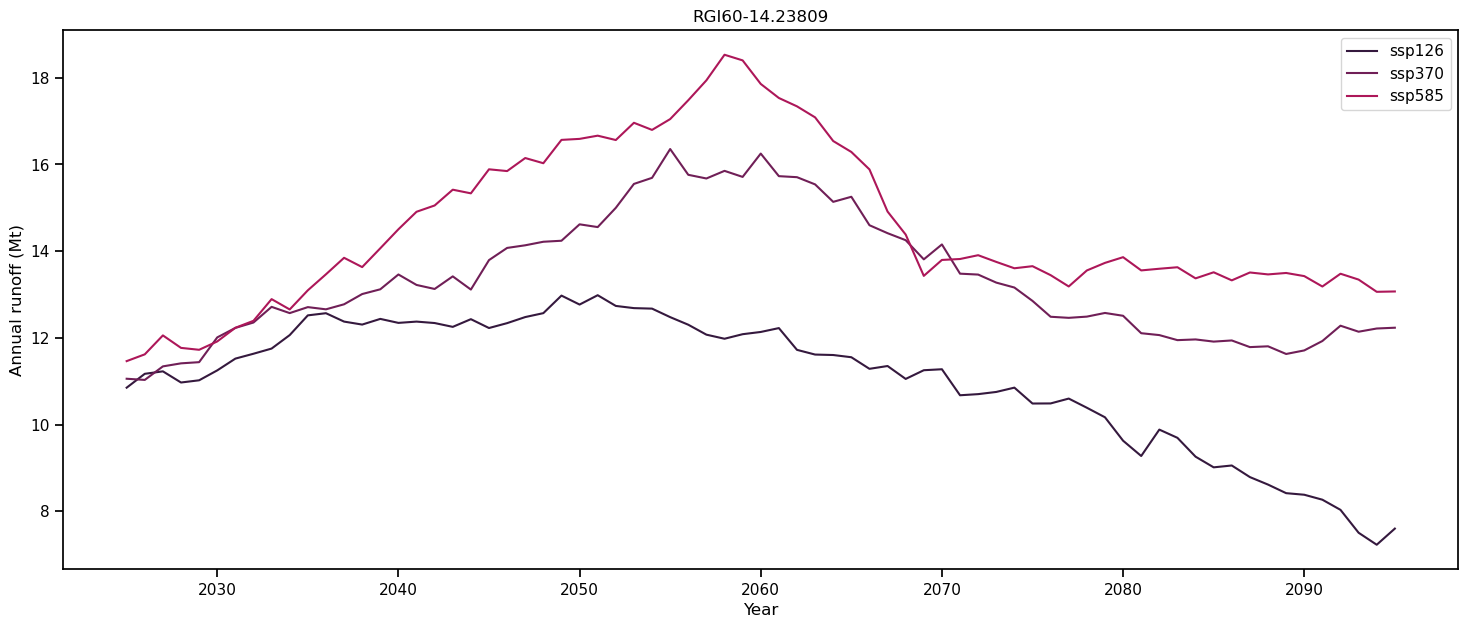
Unlike for Hintereisferner, these projections indicate that the annual runoff will increase in all the scenarios for the first half of the century. The higher SSP scenarios can reach peak water later in the century, since the excess melt can continue to increase. For the lower SSP scenarios on the other hand, the glacier might be approaching a new equilibirum, which reduces the runoff earlier in the century (Rounce et. al., 2020). After peak water is reached (SSP126: ~2050, SSP585: ~2060 in these projections), the annual runoff begins to decrease. This decrease occurs because the shrinking glacier is no longer able to support the high levels of melt.
Take home points#
Glaciers in equilibrium are not net water resources: they gain as much mass as they release over a year.
However, they have a seasonal buffer role: they release water during the melt months.
The size of a glacier has an influence on the water availability downstream during the dry season. The impact is most important if the (warm) melt season coincides with the dry season (see Kaser et al., 2010).
When glaciers melt, they become net water resources over the year. “Peak water” is the point in time when glacier melt supply reaches its maximum, i.e. when the maximum runoff occurs.
References#
Kaser, G., Großhauser, M., and Marzeion, B.: Contribution potential of glaciers to water availability in different climate regimes, PNAS, 07 (47) 20223-20227, doi:10.1073/pnas.1008162107, 2010
Huss, M. and Hock, R.: Global-scale hydrological response to future glacier mass loss, Nat. Clim. Chang., 8(2), 135–140, doi:10.1038/s41558-017-0049-x, 2018.
Marzeion, B., Kaser, G., Maussion, F. and Champollion, N.: Limited influence of climate change mitigation on short-term glacier mass loss, Nat. Clim. Chang., 8, doi:10.1038/s41558-018-0093-1, 2018.
Rounce, D. R., Hock, R., McNabb, R. W., Millan, R., Sommer, C., Braun, M. H., Malz, P., Maussion, F., Mouginot, J., Seehaus, T. C. and Shean, D. E.: Distributed global debris thickness estimates reveal debris significantly impacts glacier mass balance, Geophys. Res. Lett., doi:10.1029/2020GL091311, 2021.


