Accumulation, ablation, mass Balance and the resulting ice flow#
Goals of this notebook:
Gain a basic understanding of accumulation, ablation and glacier mass balance
Understand the link between mass balance and ice flow
Implement a simple experiment to calculate ice flow on a glacier in equilibrium
from oggm_edu import Glacier, MassBalance, GlacierBed
Copyright notice: the following sections are heavily based on the book “The Physics of Glaciers” by Cuffey and Paterson, (2010). The glacier images are taken from the open glacier graphics on OGGM-Edu, made by Anne Maussion, Atelier les Gros yeux.
The mass balance is the result of several processes that either add mass to the glacier (accumulation) or remove mass from the glacier (ablation).
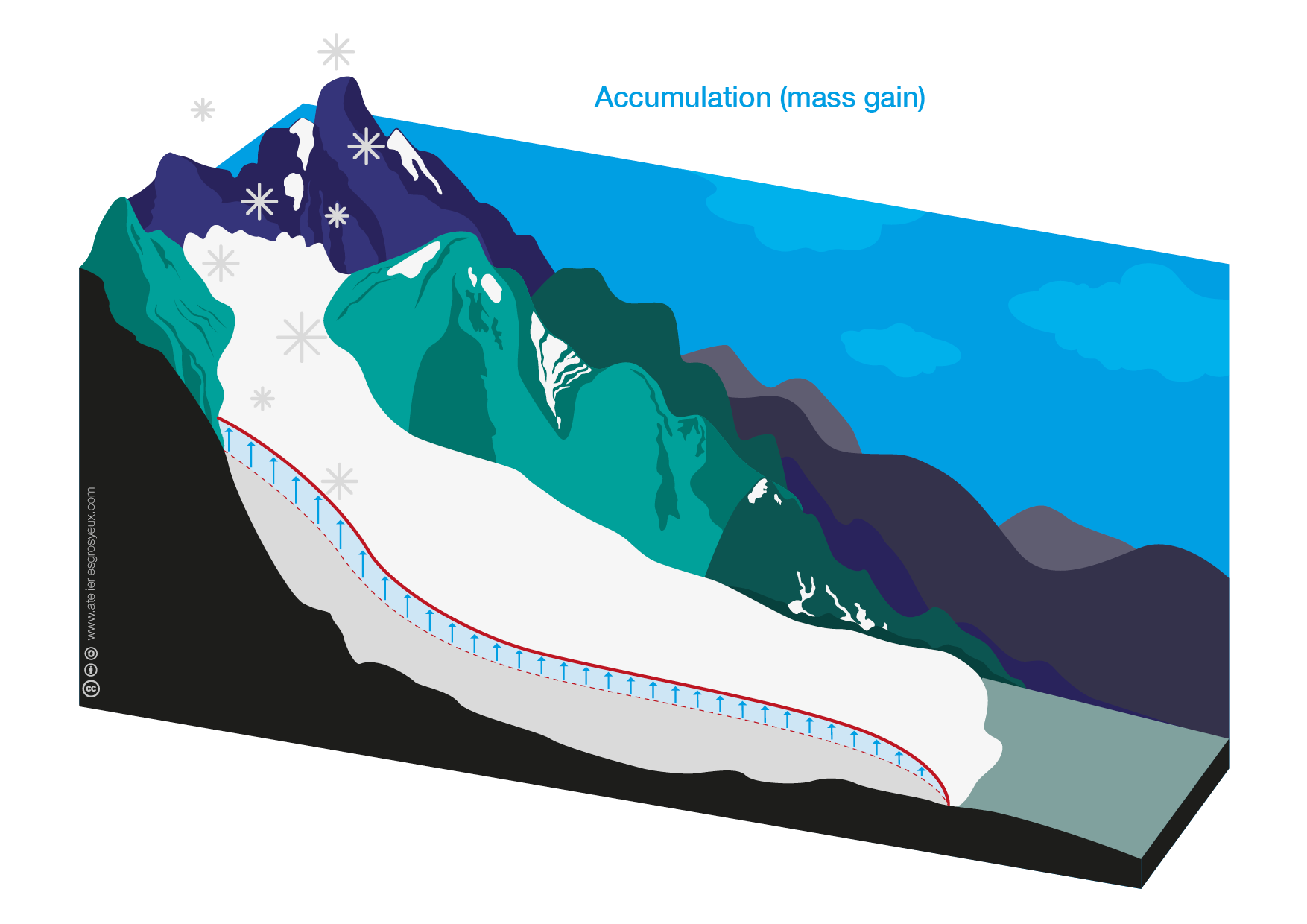
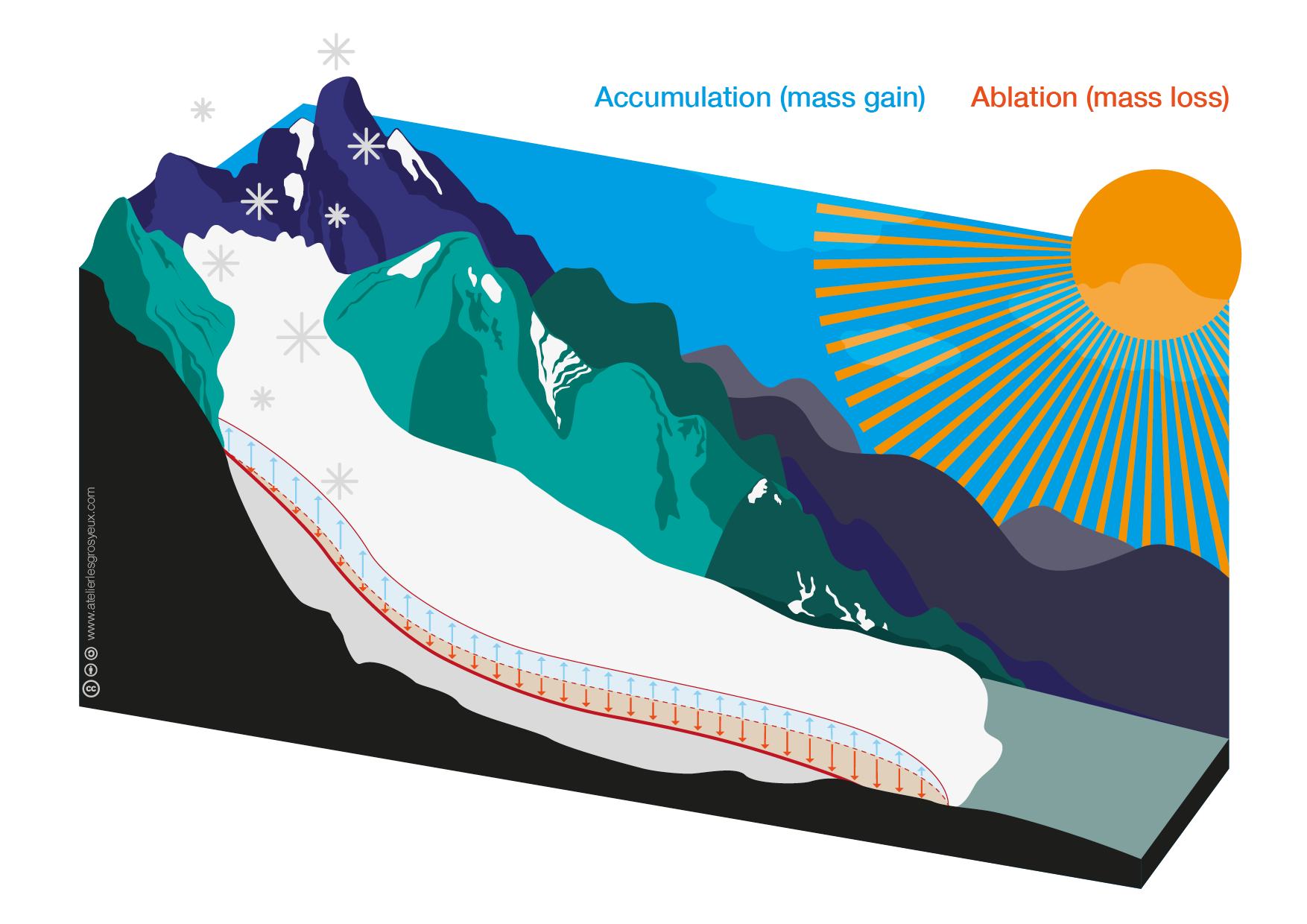

Accumulation processes#
Accumulation processes are all processes that add snow or ice to a glacier (surface). The most important accumulation processes are listed below in order of their relative importance:
Solid precipitation (snowfall)
Snowfall varies substantially with latitude and altitude, where the primary factors determining snowfall rates are:
Water vapor content governed by the Clausius-Clapeyron-relationship: the warmer the air, the more water it can hold and hence the more precipitation can form
Stratification of the atmosphere: a subfreezing layer in the lower atmosphere is required for precipitation to reach the ground in solid form
Cooling rate: high snowfall rates occur where snow is rapidly cooled, e.g. in frontal systems or via orographic lifting
Redistribution by wind and avalanching
Accumulation may differ from snowfall due to winds advecting snow over a glacier surface - the interaction between wind and the topography creates regions of snow assimilation and deposition. Furthermore, avalanches may accumulate unusually large amounts of snow in favorable zones. Avalanching is particularly important for mountain glaciers in steep valleys.
Refreezing of meltwater
Refreezing of meltwater can either occur at the glacier surface or inside the glacier body, where it is commonly called englacial or internal accumulation. Refreezing meltwater does not explicitly contribute to glacier mass balance, but it has to be subtracted from the total melt to assess the net runoff.
Deposition
Deposition refers to processes directly accumulating water or water vapor to the glacier surface, i.e. freezing rain and resublimation.
Ablation processes#
Ablation processes are all processes that remove snow or ice from a glacier. The most important ablation processes are listed below in order of their relative importance:
Melt and runoff
Melt and runoff account for most glacier mass loss and are driven by the net energy imbalance between the atmosphere and the glacier surface. The most important contributors are the net radiation and the turbulent fluxes of sensible and latent heat. Once the temperature of the glacier surface is at the melting point, i.e. the glacier surface was sufficiently heated, melts rates increase in proportion to the net energy flux.
Sublimation
Sublimation refers to the phase change from solid state to gaseous state, e.g. the direct transition of snow and ice to water vapor. It is the dominant source of mass loss in environments where surface temperatures hardly reach the melting point. Sublimation increases with increasing surface temperature and wind speed and with decreasing humidity, hence, it is strongest in dry and warm environments. Melt and sublimation can counteract each other: as sublimation consumes energy and transforms it to latent heat, the energy available for melt decreases.
Calving
Calving is the separation of ice blocks from a glacier’s margin. Most calving occurs at margins of glaciers that stand or float in water. Calving of glaciers terminating in the ocean, so called tidewater glaciers, accounts for much of the mass loss, e.g. for more than 90% of the ablation from Antarctica and about half of the ablation from Greenland. The process is also significant for mountain glaciers that terminate in deep lakes or the ocean.
This nice graphic from antarcticglaciers.org summarizes the different accumulation and ablation processes:
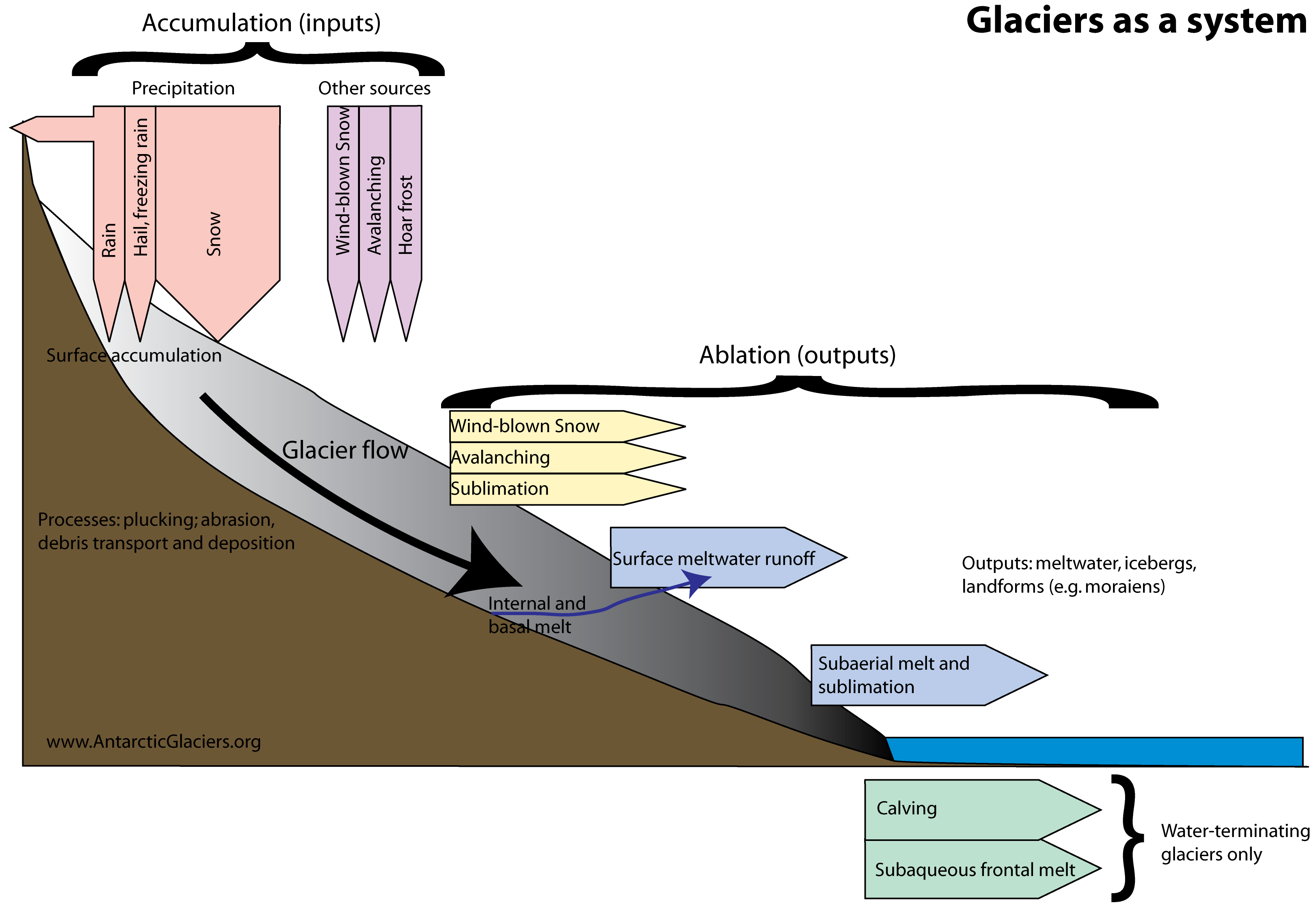
Mass balance#
The rates of accumulation and ablation processes, summed over the glacier and over time, determine the glacier mass balance: \(\dot{m}\), the change in total mass of snow and ice,
Mass is continuously redistributed in a glacier: accumulated mass at the top of the glacier is transported downglacier, which is indicated by the black arrow in the figure above. The driving force of this ice flow is gravity. Thus, the mass balance of a region on a glacier depends not only on the mass exchanges induced by accumulation and ablation, but also on the gravity driven transport of ice from the acccumulation area to the ablation area.
Generally, mass balance and ice flux are linked via the continuity equation, which implies mass conservation,
where \(H\) is the ice thickness, \(\dot{m}\) the mass balance and \(\vec{q}\) the ice flux.
Accumulation, ablation and ice flow with OGGM#
In this example, we will essentially illustrate the OGGM-Edu glacier graphics series of images using OGGM.
Set the scene#
In the introduction on the OGGM-Edu website, a cross section of a typical mountain glacier is shown:

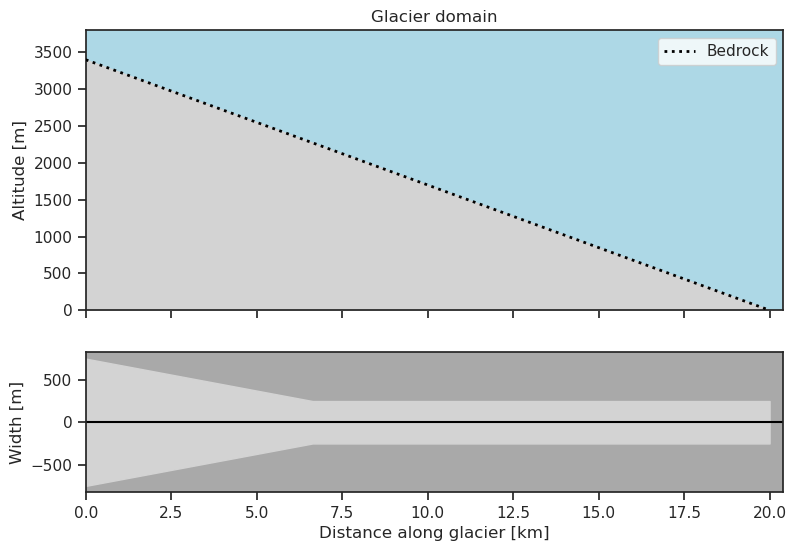
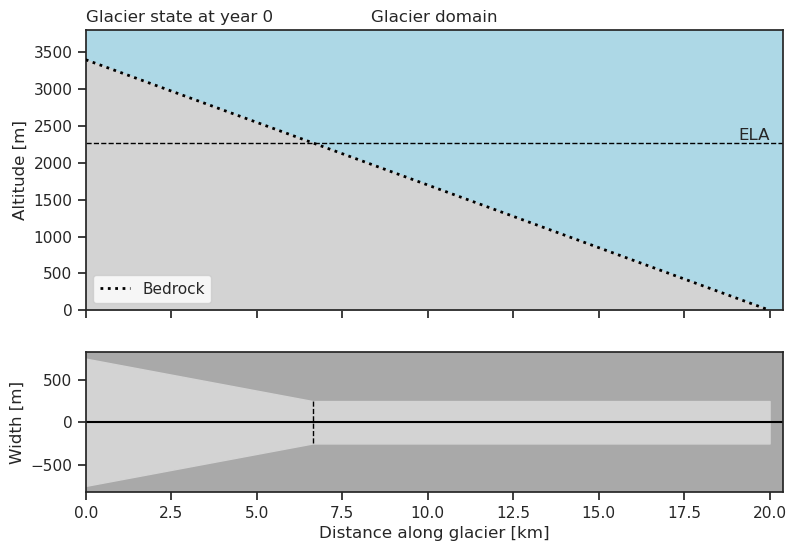
Such a glacier can be reconstructed in OGGM, as done in the intro notebook. First, we define a linear bedrock profile with a wider accumulation area, typical for mountain glaciers. The accumulation area is determined by the width at the top of the glacier, the width at the equilibrium line altitude and the vertical extent downglacier.
We want to create a glacier bed that is 1500 meters wide at the top and 500 meters wide from the ELA and down. We also want the accumulation area to make up 1/3 of the total vertial extent of the glacier.
# We define a bed with a cone shape accumulation zone and a
# square ablation zone.
top = 3400
bottom = 0
wide_narrow_bed = GlacierBed(altitudes=[top, (top-bottom) * 2/3, bottom],
widths=[1500, 500, 500])
Let’s plot the geometry of the glacier
wide_narrow_bed.plot()
Then we will need a mass balance. In our case this will be a simple linear mass balance, defined by the equilibrium line altitude (ELA) and a linear mass balance gradient with respect to elevation (in [mm m\(^{-1}\)]). The equilibrium line altitude is located at the transition between the accumulation and ablation zone. We can use the same expression as we used to create the transition for the bed:
# Since we have full control over the altitude and width we easily
# specify the ELA to match a certain transition.
mass_balance = MassBalance(ela=(top-bottom)*2/3, gradient=3)
Now that we have all the ingredients to initialise the glacier.
glacier = Glacier(bed=wide_narrow_bed, mass_balance=mass_balance)
glacier.plot()
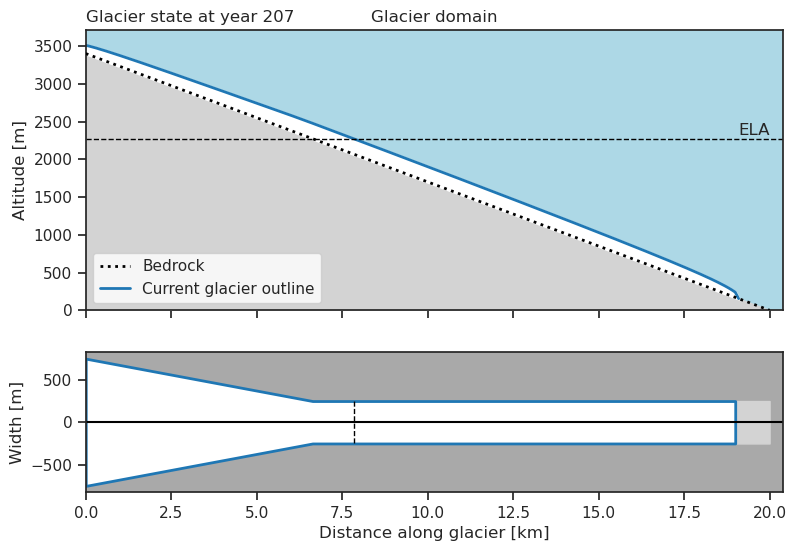
Let’s progress the glacier to equilibrium
glacier.progress_to_equilibrium()
And lets plot it
glacier.plot()
# Your input
Mass balance of a glacier in equilibrium#
For a glacier to be in equilibrium, we require the specific mass balance (accumulation + ablation) to be zero averaged over a year on the glacier. To check this requirement, we can use the mass balance model to compute the annual mass balance and compute a width weighted average over all altitudes:
glacier.specific_mass_balance
-0.48756623584850356
At the end of the year the total specific mass-balance is zero, but this doesn’t mean that the mass-balance is zero everywhere! A very classic situation looks like the image below: positive mass-balance at the top (more accumulation, less ablation) and negative at the tongue (less accumulation, more ablation).

Ice flux along a glacier in equilibrium#

In equilibrium, the ice thickness \(H\) does not change with time and the continuity equation reduces to,
This means that glacier mass balance solely determines ice flux if the glacier is in steady-state. Hence, the ice flux can be computed by vertically integrating the mass balance - in the one-dimensional case, the ice flux is the sum of the mass balance above a certain reference height \(z\).
The ice flux can then by computed by discrete integration of the mass balance.
For this example we are going to go outside the built in capabilities of oggm_edu.Glacier.
This also shows how you can access properties of the Glacier and create your own plots.
# import matplotlib
from matplotlib import pyplot as plt
import numpy as np
# We compute the ice flux from the mass balance, widths and the resolution.
# We take the cumulative sum.
mb = glacier.mass_balance.get_annual_mb(glacier.current_state.surface_h)
# Multiply by the widths (converted to meters) and resolution to get
# the grid point mass balance
mb = mb * glacier.bed.widths * glacier.bed.map_dx *\
glacier.current_state.dx_meter
# Integration
q = (mb).cumsum()
# Create a plot
fig, ax = plt.subplots()
ax.plot(glacier.bed.distance_along_glacier[q>0], q[q>0])
# Add a vertical line indicating the ELA x location.
idx = np.argmin(np.abs(mb))
ax.axvline(glacier.bed.distance_along_glacier[idx], c='k')
ax.text(glacier.bed.distance_along_glacier[idx]-0.1, 0, 'ELA',
ha='right')
ax.set_xlabel('Distance along glacier [km]')
ax.set_ylabel('Ice flux $q$ (m$^3$ s$^{-1}$)');
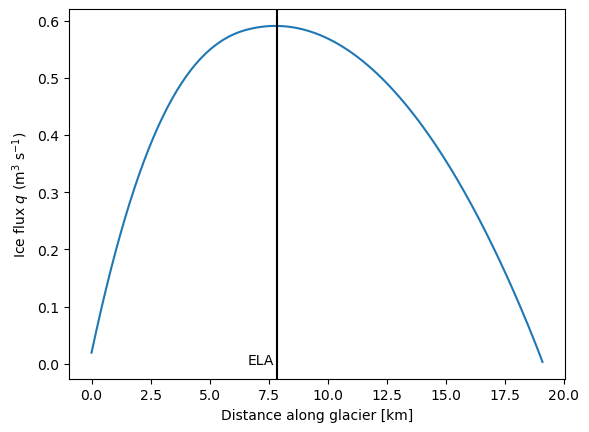
By construction, the ice flux is maximal at the equilibrium line altitude and zero at the glacier terminus.
Take home points#
Accumulation processes include all the processes that add snow or ice to a glacier, e.g.
Solid precipitation
Redistribution of snow by wind and avalanching
Refreezing of meltwater
Resublimation and freezing rain
Ablation processes are all processes that remove snow or ice from a glacier, e.g.
Melt and runoff
Sublimation
Calving
Accumulation and ablation rates determine the glacier mass balance, i.e. the change in total mass of snow and ice.
Glaciers flow due to gravity
Mass conservation implies a link between ice thickness, mass balance and ice flow
References#
K.M. Cuffey and W.S.B. Paterson, (2010), The Physics of Glaciers


